Capital Budgeting Practice Problems
The projects Net present value with various discount rates will be as follows:
The internal rate of return is the rate which leads to break even. It leads to a net present value of zero. The internal rate of return for the project is 45.72%. The modified internal rate of return can be calculated by assuming that the initial investment of $ 400,000 was borrowed at 7% which was reinvested at 10% in the subsequent years. The MIRR is thus 0%.
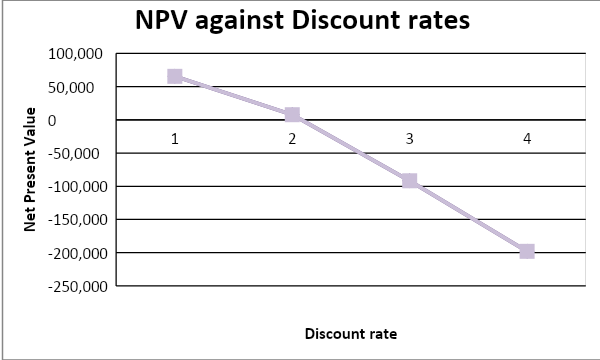
The point at which the curve meets the horizontal axis represents the IRR which is 45.72
The internal rate of return for the project is 4.41%
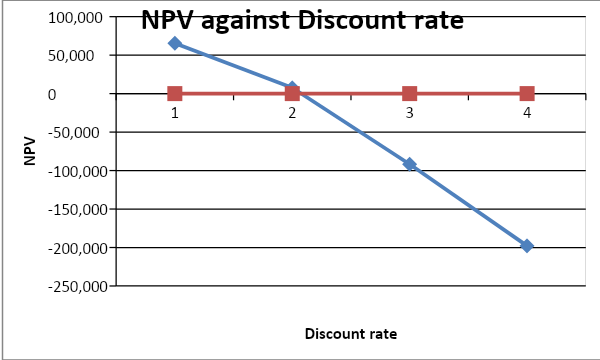
The point at which the chart intersects the horizontal line is the IRR and it is 4.41%.
- Profitability index = Net present value/ Initial investment
- 0.94 = Present value/$ 4.2 million
- Present value = 4.2*0.94 = 3.948 million
- Net Present Value (NPV) = Present value – Initial investment
- NPV = 3.948 – 4.2
- NPV = -0.252 Million
The Method That Is Best Suitable For Making Capital Budgeting Decisions
The net present value (NPV) method of project appraisal is the most suitable method for making capital decision models compared to internal rate of return (IRR) method (Dayananda, 2002). The main reason for this is that the IRR uses only one rate for evaluating all the investments while the NPV is able to use various rates. The IRR method is thus unsuitable for the comparison of projects with different cash flow timings and different discount rates. NPV on the other hand can be used to rank projects with different cash flow timing and different discount rates (Anthes, 2003).
The IRR method is a classification method and can not be used to compare two or more projects. It only seeks to determine whether a project is profitable or not without determining which project is better than the other. The IRR method can also not be applied in projects with non-conventional cash flows. These are projects with a mixture of both positive and negative cash flow. NPV can be used for such projects (McCracken, 2005).
The IRR is also hard to calculate since it involves a search of a discount rate that equates the present value to the initial investment. This is difficult to calculate and it involves the use of trial and error method and interpolation. On the other hand, the NPV method is easier and more straightforward to calculate. The NPV method is also easier to calculate for projects involving longer periods compared to IRR (Lefley, 1997).
It is, therefore, logical to conclude that the NPV method provides a more accurate basis for comparison and making capital budgeting decisions. It enhances the comparison of various projects with different time periods and it is simple to calculate. The IRR on the other hand is hard to compute and it can not be used for comparison of projects with different cash flow timings and different discount rates (Riahi-Belkanoui, 2001).
References
Anthes, G. (2003). ROI guide: Net present value. Web.
Dayananda, D. (2002). Capital budgeting: financial appraisal of investment projects. Cambridge: Cambridge University Press.
Lefley, F. (1997). Modified internal rate of return: Will it replace IRR? Web.
McCracken, M.E. (2005) Capital budgeting. Web.
Riahi-Belkaoui, A. (2001). Evaluating capital projects. Westport: Greenwood Publishing Group.