Introduction
Harry Max Markowitz is today considered as one of the most prominent American economists. This is because he conducted critical research that transformed the nature of American investments. In 1995, he wrote a Ph. D. thesis on portfolio theory while he was pursuing his studies at the University of Chicago. Markowitz clinched the 1990 Nobel Prize because of his profound research in economics that brought significant changes in investment activities. Besides this, Markowitz has maintained his profile in research by publishing various books, and articles on investment.
Markowitz formulated a theory called Modern portfolio theory. This theory gained prominence from 1950s, and it improved mathematical modeling in financial activities. Markowitz’s theory aims at maximizing the rate of return for a certain quantity of portfolio risk. Alternatively, portfolio theory can also reduce the risk that may arise in the expected return. This is achieved through proper determination of asset proportions. “The fundamental concept behind modern portfolio theory is that the assets in an investment portfolio should not be selected individually, but on their own merits” (Elton, 1995).
Risk and Expected Return
Modern portfolio theory has the assumption that investors are in most cases risk averse. This implies that when you provide investors with a choice of two portfolios which have the same level of return, they will pick the one with less risk. “Therefore, an investor can only accept increased risk if he or she expects higher returns” (Cochrane, 2005). On the contrary, an investor that needs high returns should be ready to face more losses. “The exact trade-off will be the same for all investors, but different investors will evaluate the trade-off differently based on individual risk aversion characteristics” (Elton, 1995). This means that keen investors will always prefer portfolios with favorable profiles to those with low returns and high risks. “The theory applies standard deviation of return as a substitute for risk, which is valid if asset returns are elliptically distributed” (Dufffie, 2001).
Expected return can be calculated as follows using the formula stated below.
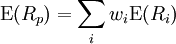
- Rp Represents portfolio returns.
- Ri Represents the asset returns.
- i and wi is the valuing of component asset.
Diversification
One of the mechanisms through which investors can mitigate portfolio risks is through holding various instruments that are not well positively correlated. This implies that possession of diversified portfolio assets can cushion an investor from individual asset risks. Diversification can also enable an investor to gain the expected return on portfolio, but with minimum risk. “It is imperative to consider price changes in each asset compared to price changes in other assets in the same portfolio” (Chincarini, 2006). “Investing is a trade off between risk and expected return” (Markowitz, 1991). Modern portfolio theory also provides guidelines for choosing low risk portfolios. Therefore, modern portfolio theory is a type of diversification (Markowitz, Portfolio Selection, 2009).
This theory explains the viable means of finding best diversification strategies. The idea of diversification as applied in this case involves choosing a group of investment assets, which together have lower risks compared to individual asset. “For instance, as prices in the stock market tend to move independently from prices in the bond market, a collection of both types of assets can therefore have lower overall risk than either individually” (Sharpe, 2008). Nonetheless, diversification has the capacity to reduce losses even if proceeds on assets are not correlated negatively and also if they are correlated positively.
Hedging is not supposed be confused with diversification. Hedging refers to offsetting risks. Risks are correlated in the case of diversification, while hedging involves negative correlations. “A common misperception is the notion that the more uncorrelated risks a portfolio is exposed to, the lower that portfolio’s overall market risk will be” (Cochrane, 2005). However, this is wrong in the sense that leveraging a portfolio with an aim of taking new risks might lead to increase in risks. Portfolio theory is mainly concerned with optimization of portfolios by investors through diversification (Markowitz, Portfolio Selection, 2009).
Mutual Fund Theorem
“Mutual fund theorem when applied in MPT means that in some cases, the optimal portfolio of an investor can be developed by holding some mutual funds in proper ratios” (Markowitz, Portfolio Selection: Efficient Diversification of Investments, 1991). In this case, the mutual funds are considered to be smaller compared to the amount of individual assets. Mutual funds in this case means specified benchmark portfolio that belongs to the available assets. Mutual fund theorem has these advantages. First, an investor can have a good chance to obtain a smaller quantity of mutual funds instead of acquiring several assets individually. This is possible if the conditions set are met. “Secondly, if it can be assumed that the relevant conditions are met, then implications for the functioning of asset markets can be derived and tested” (Dufffie, 2001). If an asset that is risk free is absent, an investor can still obtain efficient portfolio. This is possible even if efficient mutual fund is all that is accessible.
Risk Free Asset
An asset that is risk free is hypothetical, and it pays a rate that is risk free. For instance, short securities such as treasury bills can act as risk free assets. This is because they are able to pay a certain rate of interest that is fixed, and they usually have low default risk. An asset that is risk free has a zero variance, and this makes it risk free. Besides this, an asset that is risk free is also not correlated with other assets. This is because of the zero variance that it has. “Consequently, when a risk free asset is merged with other assets, the change in return is linearly related to the change in risk as the proportions in the combination vary” (Rubinstein, 2006).
Systematic Risk
A specific risk is a type of risk that is linked with individual asset. These risks can be minimized within a portfolio through diversification. “Specific risk is some time called unique or diversifiable risks” (Dufffie, 2001). Portfolio risk also known as systematic risk is a risk that is general to all securities. Nonetheless, it is not possible to diversify systematic risk within one market. Asset specific risk can be diversified as much as possible within a market portfolio. “Systematic risk is therefore equated with the risk (standard deviation) of the market portfolio” (Veronesi, 2010). Asset pricing can also be done through conditional models. Systematic risks in a particular market can also be controlled through a mechanism of long, and short positions that are available within one portfolio. This develops a portfolio that is market neutral.
Capital Asset Pricing
“The application of capital asset pricing model CAPM) in finance can help in determining the right rate of return for a given asset” (Elton, 1995). This happens if the asset has to be combined with a properly diversified portfolio. The model considers the sensitivity of the assets to risks that cannot be diversified or systematic risks. The rate of return for an asset is subject to the value of the asset on a given day. “This means that the price paid should ensure that return characteristics get better when adding an asset to it” (Miller, 2008). The CAPM is one of the mechanisms for pricing a particular portfolio or security. “The security market line enables us to calculate the reward- to- ratio for any security in relation to that of the overall market” (Sundaresan, 2009). In addition, “When the expected rate of return for any security is deflated by its beta coefficient, the reward-to-risk ratio for any individual security in the market is equal to the market reward-to-risk ratio, and it can be expressed as follows” (Tuckman, 2002).
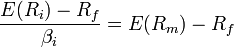
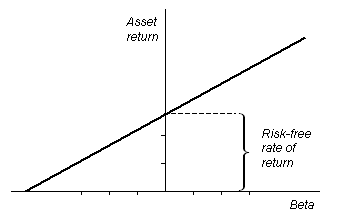
“The Security Market Line, indicated in this graph, describes a relation between the beta and the asset’s expected rate of return” (Koller & Wessels, 2010).
The CAPM is normally expressed using this formula: E(Ri) = Rf + βi (E(Rm) – Rf).
- E(Ri) – This symbol refers to the expected capital asset return.
- Rf – This symbol represents an interest rate that is risk free. For example, it can represent interest that comes from government bonds.
- E(Rm) – It shows the expected market return.
- E(Rm) – Rf – “It expresses the difference between the expected market rate of return and the risk-free rate of return” (Benninga, 2008).
- β, also known as Beta, refers to the quantification of the sensitivity of an asset to the changes in the whole market. Beta can be found through regression on past data.
When the above CAPM formula is restated as risk premium, it can be stated this way: E(Ri) – Rf = βi (E(Rm) – Rf).
The above formula shows that individual risk premium is equivalent to the market premium multiplied β.
Assumption of Modern Portfolio Theory
Modern portfolio theory has many assumptions regarding investors and markets. Some of these assumptions are explicitly described using the equations. For example, the application of normal distributions in the model returns. However, some assumptions are implicit. For instance, transaction charges, and neglect of taxes are implicit. “None of these assumptions are entirely true, and each of them compromises MPT to some degree” (Rosenboum & Perella, 2009). The assumption of modern portfolio theory is that there is fixed correlation between assets, and it remains constant. “Correlations rely on systematic relationships that occur between assets, and they are also able to adjust if these relationships under go some changes” (Tuckman, 2002). When financial crisis arises, assets are normally positively correlated, and this is because they decline together. “This implies that modern portfolio theory breaks down particularly when investors really need protection from risk” (Elton, 1995).
Second, all investors struggle to gain high economic utility. This means that investors aim at making high returns, in spite of other considerations. Efficient market hypothesis is majorly based on this assumption that modern portfolio theory relies. Third, investors are usually risk averse and also rational. “Risk aversion is the reluctance of a person to accept a bargain with an uncertain payoff rather than another bargain with more certain, but possibly lower, expected payoff” (Miller, 2008). For instance, an investor that is risk averse may decide to deposit money in a bank account that has low interests, but is guaranteed. He can pick this option instead of investing in stocks that have a potential for gaining high returns, but can still be rendered worthless. Efficient market hypothesis also reveals that real markets have information asymmetry.
Investors have a precise conception of the actual amount of returns that can be possibly got. This possibility is analyzed in behavioral finance that applies psychological assumptions to give options to the CAPM. Another assumption is that financial products usually incur transactions costs. This is likely to change optimum portfolio. The market is not modeled by Modern portfolio theory. The correlation measures, and risk returns applied by modern portfolio theory are usually based on the values that are expected. They are therefore mathematical statements concerning the future. “In practice investors must substitute predictions based on historical measurements of asset return, and volatility for these values in the equations” (Chincarini, 2006). In many cases, “the values expected fail to consider new circumstances that were not there during the development of past data” (Sundaresan, 2009). More importantly, investors mainly estimate significant parameters from historical market information. This happens because modern portfolio theory tries to analyze risk based on the probability of losses, yet it fails to give an explanation of the circumstances that may lead to losses.
The risks are actually based on probability. This is the key distinguishing factor with other methods of risk management. Fundamentally, modern portfolio theory perceives the market in terms of a group of dice. Through the analysis of previous market data a hypothesis concerning the weighting of the dice can be formulated. However, this is not important if the market relies on complicated structures. “For this reason, accurate structural models of real financial markets are unlikely to be forthcoming because they would essentially be structural models of the entire world” (Grinold, 1999). However, many individuals are acknowledging the idea of systematic risks in various financial markets, and this will probably lead to better market models.
Contribution of M PT
The modern portfolio theory can be applied in various portfolios. In the 1970s, some ideas were derived from portfolio theory, and they were applied in the domain of regional science. “Michael Conroy analyzed the variability and development in labor force” (Cochrane, 2005). The self concept that is applicable in social psychology was also modeled using the portfolio framework. “Recently, modern portfolio theory has been applied to modeling the uncertainty and correlation between documents in information retrieval” (Imanen, 2011).
Criticism of MPT
“One of the key variables required in the MPT- derived optimization algorithm is the expected return” (Elton, 1995). Expected return in put is needed in the process of initiating the algorithm. However, MPT fails to offer objective means of establishing expected return. If there is no accurate expected return, then how effective can MPT be in finding out the best asset distribution of a portfolio? “If we knew the expected return we would not need the algorithm to optimize the portfolio in the first place” (Sundaresan, 2009). Moreover, nobody can be certain about these expected returns. “The necessity of providing a subjective input in order to run an objective algorithm pushes the investor to revert to two questionable practices, that is mean reversion and trend following” (Veronesi, 2010).
A committee can be formed as an alternative means of establishing expected return. Practically, it is evident that a committee cannot prevent subjective influences that affect decision making. “There is a strong tendency for committees to develop a default estimate that assumes mean reversion” (Miller, 2008). The challenge of applying non standardized mechanisms in establishing an input variable is that it leaves the practitioner with inconsistent results. When risk is defined as standard deviation, it may provide undependable conclusions especially when one thinks of preventing risk. “Using standard deviation as a measure of risk assumes a symmetrical return distribution and assumes, absurdly, that unexpected gains are as risky as unexpected losses” (Grinold, 1999). The possibility of making unpredicted loss is the kind of risk which investors cautious about. In other words losing money is considered to be risky, but it is not risky to gain profits unexpectedly.
“Standard deviation as a measure of risk is not consistent with the way the concept of risk actually operates in investment decisions, to the degree that it assumes that risk can be measured by standard” (Koller & Wessels, 2010). Besides this, MPT does not consider the psychological characteristics that affect decision making among investors. “Consequently, a portfolio optimization algorithm that incorporates an investor’s concerns about losing money would be more appropriate than MPT’s standard deviation” (Cochrane, 2005).
Diversification removes non-systematic risk. “However, diversification forces the portfolio manager to invest in assets without analyzing their fundamentals, solely for the benefit of eliminating the portfolio’s non-systematic risk” (Dufffie, 2001). This may result into high asset prices.”The result is that the whole portfolio becomes more expensive, and the risk of the portfolio also increases” (Imanen, 2011).
Conclusion
Markowitz’s theory therefore aims at maximizing the rate of return for a certain quantity of portfolio risk. “The fundamental concept behind modern portfolio theory is that the assets in an investment portfolio should not be selected individually, but on their own merits” (Elton, 1995). “Another gist of MPT is that the market is hard to beat and that the people who beat the market are those who take above-average risk” (Benninga, 2008). Despite the criticisms and limitations of modern portfolio theory, it has remained important especially in financial investments. Warren Buffet contends that portfolio theory only provides guidelines on investment. However, the success of any investor is determined by his or her hard work and skills.
References
Benninga, S. (2008). Financial Modeling. New York: The MIT Press.
Chincarini, L. (2006). Quantitative Equity Portfolio Management: An Active Approach to Portfolio Construction and Management. New York: McGraw-Hill.
Cochrane, J. (2005). Asset Pricing. Berkley: Prentice Hall.
Dufffie, D. (2001). Dynamic Asset Pricing Theory. London: Oxford University Press.
Elton, E. (1995). Modern Portfolio Theory and Investment Analysis. New York: John Wiley.
Grinold, R. (1999). Active Portfolio Management: A Quantitative Approach for Producing Superior Returns and Controlling Risk. New York: McGraw-Hill.
Imanen, A. (2011). Expected Returns: An Investor’s Guide to Harvesting Market Rewards. New York: Wiley.
Koller, T., & Wessels, D. (2010). Valuation: Measuring and Managing the Value of Companies. New York: Harper Collins.
Markowitz, H. (2009). Portfolio Selection. The Journal of Finance, 7 (1), 77-91.
Markowitz, H. (1991). Portfolio Selection: Efficient Diversification of Investments. New York: Wiley.
Miller, E. (2008). Mergers and Acquisitions: A Step-by-Step Legal and Practical Guide. Berkley: Academic Press.
Rosenboum, J., & Perella, J. (2009). Investment Banking: Valuation, Leveraged Buyouts, and Mergers and Acquisitions. New York: Wiley Finance.
Rubinstein, M. (2006). A History of the Theory of Investments: My Annotated Bibliography. New York: Wiley.
Sharpe, W. (2008). Investors and Markets: Portfolio Choices, Asset Prices, and Investment Advice. London: Princeton University Press.
Sundaresan, S. (2009). Fixed Income Markets and Their Derivatives. New York: Academic Press.
Tuckman, B. (2002). Fixed Income Securities: Tools for Today’s Markets. New York: Pentice Hall.
Veronesi, P. (2010). Fixed Income Securities: Valuation, Risk, and Risk Management. Washington. D.C: Oxford University Press.