Introduction
Today’s financial markets are more interlocked than interlinked than ever. The effects of any major economic event have the potential to sprawl globally, affecting local economies and transforming the global economy on the whole.
The last few decades have been marked with unprecedented economic volatility that has compelled the world’s leaders to seek ways to revitalize and strengthen state economies. Himpler (2018) writes that in the last five decades, about forty events occurred that somehow displayed traits of a financial crisis. Probably, the harshest blow to the global economy was the world financial crisis (WFC) of 2008 whose ramifications have yet to fade out and cease to impact macroeconomic trends today.
The 2008 WFC started in the United States and soon was recognized as an unprecedented event of economic wealth destruction within a limited time period. Today’s literature concurs that the global crisis of 2008 has been the worst since the Great Depression in the 1930s (Bancel & Mittoo, 2011; Trabelsi, 2011).
A lot of adverse factors and events amassed before the eruption: faulty regulation, bad management of a subprime residential mortgage market innovation, and a bubble in the US housing market (Mishkin, 2010; Wallison, 2016). Over the span of two months – between July and August 2007 – 40% of the wealth on the global financial markets, or $10 trillion, was irredeemably lost.
The great adversity swayed global financial markets and exerted a profound impact on many aspects of life beyond economics. During the 2008 world financial crisis, the US GDP decreased by 30%. Japan was hit as hard as other industrialized countries of that time: its economy, previously ranked third globally, dropped below China. It shrunk 3.3% in fiscal 2008 while the trade deficit amounted to ¥223 billion in November 2008 and surged to a record ¥952.6 billion in January 2009 (Kawai & Takagi, 2011).
In February 2009, the International Monetary Fund (IMF) announced that Japan was in a deep recession (Kawai & Takagi, 2011). Arguably, Australia weathered the 2008 world financial crisis better than many other economies. Kim (2009) reports that the Pacific country faced a crisis in financial health: devoid of debt, showing steady economic growth, owning significant assets, and boasting surplus budgets. According to Hill (2012), it was the robust foundations and favorable terms of trade that allowed Australia to fare so well amidst the global financial crisis and experience a lesser shrinkage of GDP as compared to some other countries.
Economic recession, especially caused by major adverse economic events, primarily finds reflection in GDP – gross domestic product. The examples of three large economies – the United States, from where the 2008 WFC stemmed originally, Japan, and Australia – show that GDP responds to macroeconomic trends (da Silva et al., 2016).
The countries demonstrated resilience after events bearing traits of the financial crisis, with the first indicator of revitalization being an increased GDP. In the years to come, the United States, Japan, and Australia were able to overcome shrinkages and raise the GDP growth rate back to pre-crisis figures.
Indeed, monetary policy, whose success positively affects GDP, is a long-term determinant of the economic health of a state. Arguably, it was a suitable, timely, and appropriate monetary policy that put recession in the selected countries to a halt and held back the chaos. For instance, today, it has been established that it was the monetary policy, which included government stimulus, support of first-time home buyers, and other measures, that helped Australia to fare well in the face of adversity (Liu et al., 2016).
Similarly, the United States was able to escape the rut through allowing then-unprecedented bailouts and stimulus in 2008, which restored residents’ faith in paper markets and let bank customers make withdrawals (Chen et al., 2016). Even based on these findings, it is safe to assume that monetary policy is key to economic resilience: in times of crisis, it can make it or break it. In turn, GDP, and especially its growth rate as it is the change that bears the most importance, shows the real effectiveness of the monetary policy.
The question arises, however, whether monetary policy is the end-all-be-all of financial health. Indeed, its effect is profound, but one may wonder how widespread it is and what other economic aspects are affected by favorable GDP positive growth. This paper seeks to pinpoint the effects of GDP on the real interest rates and the number of stocks traded in three large economies: the United States, Australia, and Japan. The three countries are from three different regions including North America, Oceania, and Asia. Also, they are all big economic entities and ranking high over the world.
Currently, the US economy is the world’s largest: in 2019, its GDP amounted to a whopping $21.44 billion, which translates into 24% of the world’s GDP. With a GDP of approximately $5.71 trillion, Japan ranks third and takes up 6.02% of the global GDP. Lastly, as of 2019, Australia ranks thirteenth, taking up the position between South Korea and Spain. Worth $1.32 trillion, Australia’s GDP makes up 1.64% of the world’s total production.
All the selected countries are regularly using monetary policy to boost their economic market but also display certain differences. Thus, they can work as representatives to show the features of monetary policy. Literature suggests controversial implications about the relationships between the three variables, which the current research aims to elucidate further.
The rest of the paper is organized as follows. The literature review defines the key terms and concepts used in the current study: GDP and GDP growth, real interest rate, and stocks traded. Cited literature describes the relationships between variables as discovered by other researchers. Methodology discusses and justifies the chosen study design, operationalizes variables, and addresses the ethical considerations of research.
Data analysis covers the mathematical underpinnings and statistical methods used for making sense of numerical data samples for the current study. It is in the results section that the study’s findings can be found, including tables and figures for comprehensive and understandable data visualization. Lastly, the discussion section compares the study’s findings to the existing body of research, and the conclusion recapitulates the main implications.
Literature Review
GDP and GDP Growth
The abbreviation GDP stands for the gross domestic product; it is used for the measurement of the monetary value of goods and services produced in a country within a particular time period. The GDP takes into account only the so-called final goods and services – those that have been purchased by the final user.
Broadly, GDP consists of goods and services produced for sale in the market; however, some nonmarket production such as education or healthcare provided by the state is also included. GDP is not to be confused with GNP: the alternative concept takes into consideration strictly the output of the residents of a given state, ignoring national organizations’ overseas subsidiaries and franchises.
GDP is a key concept and a metric instrumental in evaluating the economic performance of a given country. Landefeld et al. (2008) refer to measuring the GDP to “taking the pulse” of the economy. The question arises as to how GDP is constructed, what its limitations are, and why it often draws a picture different from what other commonly used economic metrics display. The creation and development of the concept of GDP in the United States were motivated by the profound, unprecedentedly adverse changes caused by the Great Depression in the 1930s (Lepenies, 2016).
Over the decades, the notion of GDP and its theoretical and mathematical underpinnings evolved to serve the changing needs of the country (Coyle, 2015). At present, economists use multiple approaches to measuring GDP that can be broadly categorized into three groups: value-added (or production) approach, income (by type) approach, and final demand (or expenditures) approach (Landefel et al., 2008).
Income (by type) approach
The income (by type) approach allows us to calculate total domestic incomes earned. Roughly speaking, the income approach sums all incomes generated by production: compensation, rental income, profits and proprietors’ income, taxes on production, and others;
Expenditure approach
The expenditure approach to computing gross domestic product (GDP) considers the sum of all final goods and services bought in an economy over a particular time span. That entails all consumer spending, state spending, business investment spending, net exports, and others;
Value-added approach
The value-added approach helps to calculate the “value-added” at each stage of production. Within this method, it is assumed that value-added is the difference between total sales and the value of intermediate inputs required for the production process. Indeed, the main advantage of the input-output approach lies in its ability to enforce consistency and reconcile data on commodity outputs, inputs, and final demand (Landefeld, 2008). The current research uses the GDP data calculated using the value-added approach.
Despite its long history and consistent use that persisted into today’s age, as a key economic metric, GDP faces serious challenges. The rise of digital technologies – the advancement of digital innovation, the advent of cloud computing, and the development of artificial intelligence – continues to change the business environment and people’s daily lives (Tapscott, 2015).
Watanabe et al. (2018) opine that GDP statistics might not be robust and adaptable enough to capture the advancement of the digital economy. In particular, Ahmed and Schreier (2016) name multiple “production loops” that might be skewing GDP metrics in the digital age:
- new types of intermediation of peer-to-peer services;
- blurring production boundaries allowing consumers to become producers;
- consumer durables and investment;
- free, “freemium,” and subsidized consumer product;
- household-produced free assets;
- e-commerce transactions that are difficult to track;
- miscalculations of ICT prices.
Given the current challenges of using GDP, the question arises as to what justifies its use for the current research. GDP does not yet lose its importance because it provides information about the size of the economy and its overall importance. It is believed that changes in GDP are suggestive of the health of the economy on the whole. Broadly speaking, an increase in real GDP (GDP adjusted for inflation) is seen as reflective of positive economic trends while the opposite is also true: a decreased GDP is a sign of a shrinking economy.
Despite the limitations of the metric and its occasional imprecision, the figures that the method produces do not show a non-negligible discrepancy from what is happening in the economy. For instance, GDP metrics dipped across the board during the Global Economic Crisis of 2008, which is an explainable and logical occurrence.
Real Interest Rate
A real interest rate is defined as an interest rate that is reflective of the real cost of funds to the borrower and the real yield to the lender or an investor. Calculating a real interest rate implies certain adjustment to remove the effects of inflation (Daniels et al., 2019). In a more formal way, a real interest rate can be described using the Fisher equation: (1 + i) = (1 + r) (1 + π) where i is the nominal interest rate, r is the real interest rate, and π – the inflation rate.
The more commonly used version is an approximation of the previous formula: i ≈ r + π. A simple example would be locking a 10% interest rate for the next year and anticipating a 5% rise in prices. Substituting variables with the given figures, it is easy to see that the real interest rate, in this case, would be equal 10 – 5 = 5%.
The nominal interest rate should be understood as the interest rate that is paid on a loan or investment. In turn, the best way to explain the real interest range is to interpret it as a reflection of the change in purchasing power derivative from an investment or given up by the borrower (Barnes, 2016).
It is critical to adjust the nominal interest rate to compensate for the effects of inflation as it allows for pinpointing the shift in purchasing power of a particular level of capital over a certain time period (Barnes, 2016). The time-preference theory of interest provides its own take on the interpretation of the real interest rate (Barnes, 2016). According to the time-preference theory of interest, the real interest rate shows the degree to which consumers prioritize current goods over future goods (Mishkin, 1981; Mishkin, 1982).
A borrower who would like to make use of funds in the present is likely to have a stronger time-preference for current goods as opposed to future goods. In a similar fashion, a lender who envisions consumption in the future has a lower time-preference and is likely to loan funds at a lower rate. When one adjusts an interest rate for inflation, what is ultimately revealed is the rate of time-preference among market participants.
The Fisher equation finds application in several domains such as cost-benefit-analysis, Inflation-indexed bonds, and monetary policy. The Fisher equation plays an important role in proving the Fisher’s hypothesis, also commonly referred to as the Fisher effect (Caporale & Gil-Alana, 2019). The Fisher hypothesis states that the real interest rate is not contingent on monetary measures and in particular, the nominal interest rate and the expected inflation rate.
On the other hand, researchers such as Handel et al. (1996) disprove the key hypothesis developed by Irving Fisher. Handel et al. (1996) draw on works by Mundell and Tobin, Darren and Feldstein, and Stulz and demonstrate a stable negative correlation between ex-ante real interest rates and expected inflation rates.
At present, there is an ample body of research confirming the existence and describing the relationship between the GDP growth rate and real interest rate. So far, the general consensus on the subject matter has been that an increase in real GDP (interpreted as economic growth) leads to an increase in average interest rates in an economy. Conversely, when real GDP plummets, such as during a recession, what follows is a decrease in will cause a decrease in average interest rates in an economy.
The first inquiries date back to a now-classic work by Ramsey (1928) that currently serves as a staple for macroeconomic theory. It has been long established that productivity (reflected in real GDP) can serve as a long-term predictor of return on capital and, therefore, a determinant of interest rates. Thus, it is understandable why there might be a positive correlation between these two indicators.
On the other hand, scholars such as Bergeaud et al. (2019) argue that the relationship between GDP growth and real interest rate is far from linear: to them, this linearity is only “one side of the coin.” Bergreaud et al. (2019) opine that interest rates also serve as a determinant of the minimum expected return from investment projects.
Thus, they require and promote a certain productivity rate required for such investments. Hansen and Seshadri (2014) provide an even more peculiar explanation: their longitudinal data analysis has demonstrated a moderate negative correlation between the real interest rate and economic growth. Nemat and Jalaleddin (1991) write that the idea that high real interest rates are bad for economic growth is persistent in economics. Yet, the evidence gathered between 1950 and 1990 undermines this assumption.
Interestingly enough, there exists an orthogonally different opinion that negates the idea of not only such a relationship but a relationship at all. Bosworth (2016) argues due to the high degree of integration of financial markets in the present moments, it is not reasonable to model, analyze, and predict interest rates within a closed-economy, one-country framework. According to the analysis conducted by Bosworth (2016), there is but a weak association between real interest rates and economic growth. All in all, the existing evidence is controversial, leaving some knowledge gaps to be filled.
Hence, the null and alternative hypotheses for the current study drawing on the provided theoretical underpinnings are as follows:
- H0: There is no relationship whatsoever between the real GDP growth rate and the real interest rate in either of the countries analyzed;
- H1: There is a negative relationship between the real GDP growth rate and the real interest rate in at least some of the countries analyzed;
- H2: There is a positive relationship between the real GDP growth rate and the real interest rate in at least some of the countries analyzed;
- H3: There is a positive relationship between the real interest rate and the real GDP growth rate in at least some of the countries analyzed;
- H4: There is a negative relationship between the real interest rate and the real GDP growth rate in at least some of the countries analyzed.
GDP Growth and Stocks Traded
A stock or share, also commonly referred to as a company’s equity is the representation of a person’s ownership in a company or corporation or of a claim of its assets and earnings proportionate to the number of stocks owned. In turn, a stock market is defined as a market where individual or institutional investors engage in the buying and selling of shares in a public venue. In other words, a stock market can be understood as an aggregation of buyers and sellers of stocks. A country or a region might have multiple stock trading venues where transactions in stocks and other forms of securities take place.
The relationship between the GDP growth rate and the stock market is one that has long been gaining much traction in academic and practitioners’ circles. Today, there is a longstanding consensus that the economy affects corporate earnings in terms of costs and revenue (Wang & Ajit, 2013; Antonios, 2011).
Stock prices often serve as an indicator of investor expectations for future corporate earnings and, in turn, for future economic growth. Sun et al. (2016) opine that reliable economic forecasts provide a helpful tool that can inform equity market decisions.
If, for example, an economic recovery is predicted — preferably with some degree of reliability — then this could signal an appropriate time for investing in stocks. For instance, if it is predicted that the economy is on its way to recovery, investors typically interpret it as a favorable condition and timing for investing in stocks (Sun et al., 2016). The mechanism might seem quite straightforward; however, the reality of monetary policies and stock markets paints a rather complicated picture.
In his critical piece, Sandte (2012) asks whether the economy drives the stock market or it is the expectations about the economy that impact stocks traded. Sandte (2012) concludes that apparently, there is a circular relationship between the economy and the stock market: they affect each other, and it is nigh on impossible to pinpoint which runs ahead of which. Today, it is recognized that stock market performance impacts the economy, and arguably, its leverage has only become more significant over the span of the last few decades.
In particular, Sandte (2012) discusses confidence effects as one of the primary contributing factors. Steady stock market declines are often symptomatic of economic slowdown in the nearest future. The said declines are detrimental to consumer confidence and the business outlook (Sandte, 2012).
As a result, what might take place is lower consumption and investment spending. Another concept discussed by Sandte (2012) is the “financing effect” that occurs primarily in the corporate sector. In case a company relies heavily on the stock market for financing, it is more prone to being held back by bear markets. To recapitulate, there is evidence of an alleged circular relationship between stock markets and economic growth: they impact each other in equal measure.
Levine and Zervos (1999) provide a compelling piece that seeks to answer the question of whether the financial system, of which stock markets make a part, constitutes an important impetus for economic growth. Levine and Zervos (1999) explain that there is a persistent opinion that stock markets are nothing more than “burgeoning casinos” where players make bets for their own personal benefits.
The scholars refer to other researchers such as Mayer (1988), Stiglitz (1985), and Devereux and Smith (1994) who unanimously diminish the role of stock markets in building up capital and negate their link to economic growth. Among the arguments used to support this point of view is the assumption that a great economic risk coming from integrated international stock markets is an impediment to economic growth and saving rates (Levine & Zervos 1999).
Schleifer and Summers (1988) argue that stock markets might hurt economic growth through “counterproductive corporate takeovers.” In other words, there is quite a large number of scholars who see stock markets as volatile entities that are unpredictable at best and detrimental to economic growth at worst.
To counter this approach to stock markets, Levine and Zervos (1998; 1999) empirically studied the relationship between various indicators of stock market development and long-run economic growth. The two studies focused on a variety of countries, starting with those with developed economies and ending with emerging, if not to say struggling, ones such as Haiti, Mali, Liberia, Zambia, and others. Levine and Zervos (1998; 1999) were able to demonstrate that even after controlling for many factors associated with growth, stock market liquidity and banking development were still reliable determinants of economic growth.
Apparently, there is a lack of consensus on the subject matter, which makes it compelling to entertain both points of view. All facts considered, the null and alternative hypotheses for the current study based on the provided theoretical underpinnings are as follows:
- H0: There is no relationship whatsoever between the real GDP growth rate and the amount of stocks traded in either of the countries analyzed;
- H1: There is a positive relationship between the real GDP growth rate and the amount of stocks traded in at least some of the countries analyzed;
- H2: The reverse is true: the stock market runs ahead of the economy, and there is a positive correlation between stocks traded and the real GDP growth.
Methodology
The current retrospective longitudinal study employs quantitative design: it explores numerical data, provides descriptive information pertaining to collected datasets, and seeks, identifies, and interprets relationships between variables. A quantitative design was chosen for several reasons: firstly, its high replicability means reliability and less open to debate and argument.
Secondly, numerical data allows for straightforward analysis: collected data makes it easier to draw conclusions regarding which statistical tests are appropriate to use. For this reason, interpreting data is a delineated, clear process that is less prone to bias and subjectivity. Last but not least, the concepts that are described in the literature review and researched within the scope of the current study are easily operationalized and expressed numerically, which provides even more grounds for choosing the quantitative design. For the current study, the researcher identified one independent and two dependent variables:
- GDP growth rate (IV) (annual %; under the domain of economic policy & debt, national accounts, and growth rates) collected from the World Bank national accounts data, and OECD National Accounts data files. As the source suggests, the aggregation method was weighted average, and the chosen method of measuring GDP was the value-added approach;
- Real interest rate (DV) (annual %; under the domain of the financial sector) collected from the International Monetary Fund, International Financial Statistics and data files using World Bank data on the GDP deflator. Real interest rates are calculated by adjusting nominal rates by an estimate of the inflation rate in the economy. A negative real interest rate indicates a loss in the purchasing power of the principal. The real interest rates are calculated as (i – P) / (1 + P), where i is the nominal lending interest rate and P is the inflation rate (as measured by the GDP deflator);
- Stocks traded:
- Total value (current US$) (DV) (annual; under the domain of financial sector – capital markets) sourced from the World Federation of Exchanges (WFE) database. The WFE used two approaches for generating data before the year 2001: the trading system view (TSV) and regulated environment view (REV);
- Stocks traded, total value (% of GDP) (annual %; under the domain of financial sector – capital markets) sourced from the World Federation of Exchanges (WFE) database. The method used by the WFE for the calculation of stocks traded as a share of GDP is weighted average;
- Stocks traded, turnover ratio of domestic shares (%) (annual %; under the domain of financial sector – capital markets) sourced from the World Federation of Exchanges (WFE) database. Turnover ratio is the value of domestic shares traded divided by their market capitalization. The value is annualized by multiplying the monthly average by 12.
All data used for the current study is recent: as sources suggest, the last update took place on May 28, 2020. The data spans between 1980 and 2020. The chosen sources are reliable international financial institutions with an excellent reputation. The sampled data on all three variables – GDP growth rate, real interest rate, and stocks traded is mostly complete, though some years are missing. The current study takes into consideration the ethical implications of data use. All data are publicly available and open to analysis, manipulation, and use in research as long as it does not pursue a for-profit purpose.
Data Analysis
The data analysis for the current study was done using the programming language Python, in particular with the help of libraries developed specifically for statistical analysis: NumPy, Pandas, Math, Stats, SciPy, and some others. As a dynamic, object-oriented, and easy-to-read language, Python allows for accomplishing complicated computing tasks in fewer lines of code and with more ease than many other tools. As of 2019, Python ranks as number one among programming languages in the data science domain, which includes financial computations pertaining to the subject matter of the current study.
Regardless of the computing tool chosen for the study, appropriate mathematical methods remain the same. For the current research, there will be conducted two types of analysis: descriptive and exploratory (predictive). Descriptive analysis is seen as a preliminary step and preparation for further statistical analysis.
For the chosen dataset, some of the basic statistics to be calculated are mean, median, quartiles, minimum, and maximum. A quartile is defined as a type of quantile that allows dividing the number of data points into four parts, or quarters, using the median of the data set. All these data wrangling and manipulations will help to get a hold of the basic features of the data in a study and summarize the sample and its measures in a simple fashion.
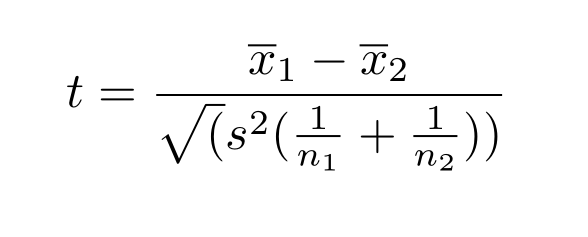
The current study also makes use of inferential statistical tools such as Student’s t-test if its assumptions are met. Student’s t-test can be used to contrast GDP growth, real interest rates, and stocks traded between countries by comparing the means of two groups picked pairwise (see Image 1). However, in case some of the datasets do not follow the normal distribution, the Wilcoxon test is administered. The Wilcoxon test is a nonparametric statistical test that serves the same purposes as Student’s t-test: it determines whether two or more sets of pairs differ from each other in a statistically significant manner.
Lastly, exploratory data analysis using simple linear regression will allow us to identify relationships or lack thereof between the chosen independent and dependent variables. Linear regression is a type of statistical modeling that attempts to find an association between two variables by fitting a linear equation to observed data. The equation takes the following form: y = B0 + B1 * x. In other words, as seen from the equation, this linear model assumes that the value of y (dependent variable) can be computed from a linear combination of the explanatory variables (X).
Results
Descriptive Statistics
Table 1. Descriptive statistics on GDP where the count is the number of observations, mean is the arithmetic average, STD is standard deviation, the minimum is the minimum value, max is the maximum value, and 25%, 50%, and 75% signify quartiles (a more detailed explanation is provided in “Data Analysis”). The country codes should be read as follows: AUS = Australia, JPN = Japan, US = the United States.
Table 2. Descriptive statistics on stock markets in the United States, Australia, and Japan.
Table 3. Descriptive statistics on real interest in the United States, Australia, and Japan.
As seen in Table 1, Australia shows the highest average GDP growth rate (3.14%). The biggest standard deviation is found in the Japanese dataset (2.24%), meaning that GDP trends are characterized by acute spurs of growth as well as recessions. Japan experienced the biggest GDP loss of 5.41% while the US had the biggest surge (7.23%) during the selected time period. Table 2 describes stock market performance in the selected countries. The United States trades the most stocks on average ($19,995,174,362,068, annual mean). In this country, the average value of stocks traded surpasses GDP by almost 50% (148%).
Lastly, the United States has the highest average turnover domestic ratio of 130. Table 3 shows that Australia boasts the highest average real interest rate of 4.97%; the country down under is the one with the highest real interest from 1980 through 2020 – 10.07%. Japan demonstrates worse performance: it has the lowest mean real interest rate (3.26%) and the minimum value during the chosen time span (-0.98%).
Inferential and Exploratory Statistics
Student’s t-test has demonstrated that there is a significant difference between Japan’s and Australia’s GDP indicators throughout the years (t-value = 2.762, p-value = 0.007, confidence level = 99.3%). Likewise, a statistically significant difference has been found between Japan’s and Australia’s turnover domestic ratio: statistic=-3.6, p-value=0.0005, and confidence level = 99.95%. Since the data on Australia’s and Japan’s real interest rates were not normally distributed, the Wilcoxon test was administered.
It showed a significant difference between the two dataset: statistic=146.0, p-value=0.0006, confidence level > 99%. In a similar fashion, there is a difference between the real interest rates in Japan and the United States (statistic=113.0, p-value=0.0001, confidence level > 99%). As for other pairs, testing for statistically significant differences did not yield any results.
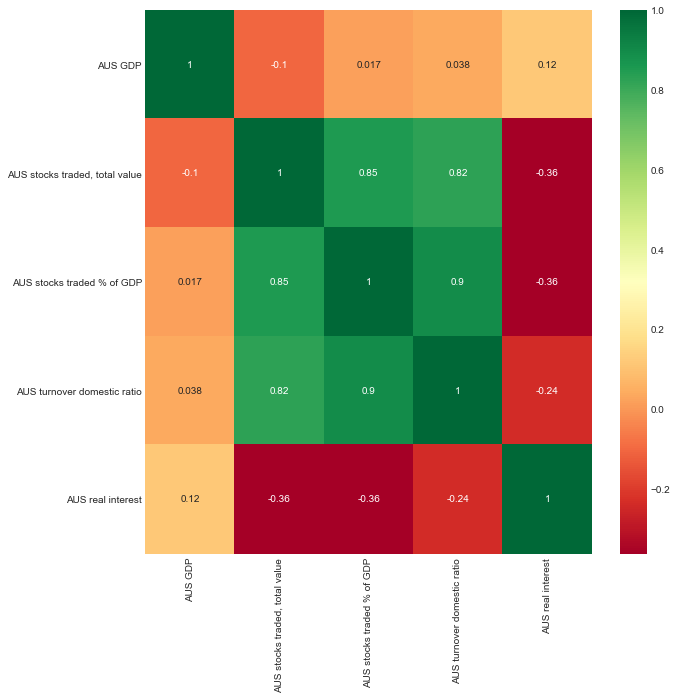
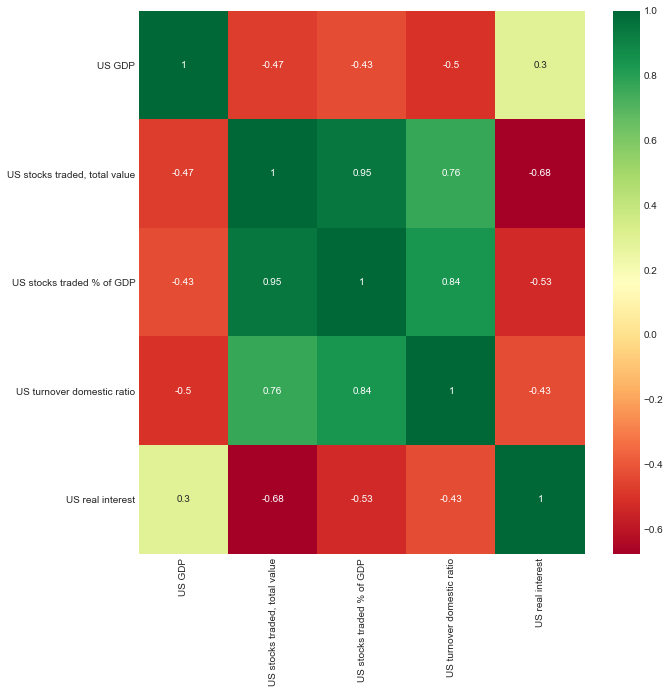
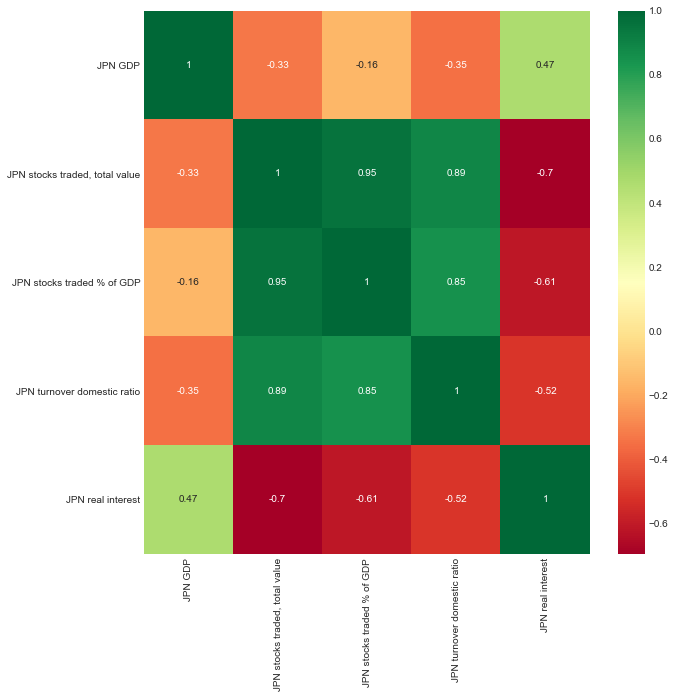

Before creating a linear regression model, basic linear regression assumptions were tested. The linear regression analysis has shown that for Australia, there was not any correlation between either of the selected variables as in none of the cases, the p-value was less than 0.5 and r-squared was no greater than 0.11.
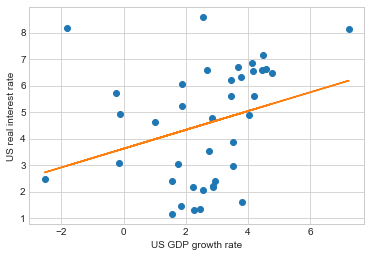
The correlation matrix that shows whether variables move in the same direction yields the same results (Figure 1). The situation is somewhat different with regard to Japan and the United States. As seen from Figure 2, the US GDP growth rate slightly correlates with the US real interest rate. Modeling yields similar results: it shows a weak relationship between the variables with r-squared = 70 and p-value = 0.01 (see Figure 4).
The data on Japan shows a reverse relationship: there, the real interest rate seems to be a determinant of the GDP growth rate (r-squared = 0.68, p-value = 0.03) (see Figure 5). The same insight is found in Figure 3 (“Correlation matrix for Japanese data”). In all three correlation matrices (Figure 1-3), it is visible that stock market performance indicators correlate with each other, with the correlation coefficient approaching 1.0. However, these findings are out of the scope of the present study and should be discussed in subsequent endeavors.
Discussion
The current study did not confirm all the alternative hypotheses put forward at the beginning of this paper. It appears that monetary policy, whose success was operationalized as the GDP growth rate, affected the real interest rate only in the case of the United States while the same was not true for the rest of the selected country.
The reverse relationship was only confirmed for Japan where, allegedly, the real interest rate contributed to economic growth. The findings of this study negate the conclusions to which Hansen and Seshadri (2014) were able to come in their research. While Hansen and Seshadri (2014) argue about the presence of a negative relationship between economic growth and real interest rate, the current study shows that the opposite might be true.
The hypothesis developed by Bergeaud et al. (2019) was confirmed only partly: the scholars insisted on the circular nature of the relationship between GDP growth rates and real interest rates. The current study demonstrated that the relationship, indeed, goes in both ways, but it was proven for two different countries – Japan and the United States. Apparently, this study’s findings are somewhat consistent with the position that Bosworth (2014) defended in his works: he spoke of only a weak relationship between these variables. Besides, according to Bosworh (2014), the very task of measuring the real interest rate was barely feasible.
Indeed, even though the current study confirms some of the hypothesized associations, the relationships are not convincing enough, given that the r-squared values do not exceed 0.70. This means that no more than 70% of data fit the model, which might as well invalidate the model altogether. Besides, Figure 4 and Fugure 5 show that the relationship between the variables is far from perfectly linear with only some data points lying on the regression line.
The current study failed to find any relationships between economic growth and stock market performance. The findings counter Sandte’s (2012) findings that pointed at the circular nature of the relationship between economic growth and stock markets and their mutual influence on each other.
If anything, it seems like the results are more in line with Mayer (1988), Stiglitz (1985), and Devereux and Smith (1994) who deny the need for a financial system, which includes developed stock markets, for stimulating economic growth. However, the current study did not discover any evidence that stock markets are “burgeoning casinos” that hurt the economy – an argument vehemently supported by scholars such as Schleifer and Summer (1988). To recapitulate, the null hypothesis that there is no relationship between monetary policy and stock markets was confirmed.
One should not rule out the possibility that the results of the study might have been impacted and compromised by bias. The greatest limitation is the very method of collecting data used for this study. The literature review section has already touched on the issues of using GDP in today’s economy where plenty of activities have become or becoming digitalized (Watanabe et al., 2018).
For this research, GDP was measured using the value-added method that has its own downsides. In many industries, value-added is inferred from the base year using single volume indexes of outputs or, less commonly, inputs. In the case of the service industry, researchers often struggle to develop well-defined measures of output, which renders evaluating the growth of services especially difficult.
Aside from that, current measures of GDP often fail to take into consideration technological improvements, which leads to an underestimation of the value of output and value-added. Lastly, the weighted average of the growth rates used by the World Bank does not necessarily reflect the GDP growth rate as the method implies rescaling using different base years.
Even though this research was not able to confirm many of the hypotheses, it lays the foundation for subsequent studies on the subject matter. It makes sense to look into metrics of economic growth other than the gross domestic product as it might have become inadequate for research of this kind. Future research might also draw a line between economic growth and economic development, which are two distinct phenomena.
Henry (1987) opines that economic development is a broader term that is also helpful for understanding the quality of life enabled by economic measures. Indeed, this variable might be an appropriate substitute for GDP that has been on a slowdown in the last couple of decades. Apart from that, future research could broaden the scope of inquiry and include not only countries but economic regions for further comparison.
Conclusion
Today, world economies are more interconnected and interlocked than ever. Yet, every country follows its own path, building upon a foundation of its own unique resources and historical predispositions. The major economic events of the end of the 20th and the start of the 21st century make it compelling to study the links between economic phenomena that they have undoubtedly shaped and impacted. The current study addressed the effects of monetary policy, whose success is reflected in GDP, on real interest rates and stock markets. Alternatively, it was hypothesized that a reverse relationship is also possible.
Only two of the hypotheses that were put forward for this study have found confirmation in the data. Namely, there is a weak relationship between the United States GDP growth rate and the United States’ real interest rate. In Japan, the real interest rate appears to be a predictor of the GDP growth rate. As for Australia, the selected variables seem not to be correlated at all. To conclude, the effects of monetary policy on real interest rates and stock markets are not universal. Real interest rates and stock market performance indicators were not found to be universally reliable determinants of economic growth either.
Reference List
Ahmad, N & Schreyer, P 2016, ‘Measuring GDP in a digital economy’, in OECD Statistics Working Papers, 2016/07, OECD Publishing, Paris.
Antonios, A 2010, ‘Stock market and economic growth: an empirical analysis for Germany’, Business and Economics Journal, vol. 2010, pp.1-12.
Bancel, F & Mittoo, UR, ‘Financial flexibility and the impact of the global financial crisis: evidence from France’, International Journal of Managerial Finance, 2011, vol. 7, no. 2, pp. 179-216.
Barnes, P 2016, Stock market efficiency, insider dealing and market abuse, CRC Press, Boca Raton.
Bergeaud, A, Cette, G & Lecat, R 2019, The circular relationship between productivity growth and real interest rates. Web.
Bosworth, B 2016, Interest rates and economic growth: are they related?. Web.
Caporale, GM & Gil-Alana, L 2019, Testing the Fisher hypothesis in the G-7 countries using I (d) techniques, International Economics, vol. 159, pp. 140-150.
Chen, Q, Filardo, A, He, D & Zhu, F 2016, Financial crisis, US unconventional monetary policy and international spillovers, Journal of International Money and Finance, vol. 67, pp. 62-81.
Coyle, D 2015, GDP: a brief but affectionate history-revised and expanded edition, Princeton University Press, Princeton.
Daniels, JP, Mazumder, S. and VanHoose, D.D., 2019. Expected inflation and the sacrifice ratio. International Finance, 22(3), pp.307-322.
da Silva, MF, Pereira, ÉJDAL, da Silva Filho, AM, de Castro, APN, Miranda, JGV & Zebende, GF 2016, ‘Quantifying the contagion effect of the 2008 financial crisis between the G7 countries (by GDP nominal)’, Physica A: Statistical Mechanics and its Applications, vol. 453, pp. 1-8.
Devereux, MB & Smith, GW 1994, ‘International risk sharing and economic growth’, International Economic Review, pp. 535-550.
Hansen, B & Seshadri, A 2013, Uncovering the relationship between real interest rates and economic growth, Michigan Retirement Research Center Research Paper, p. 303.
Henry, CM 1987, ‘Economic growth and economic development: a distinction without a difference’, Social and Economic Studies, pp. 67-84.
Hill, Jennifer G 2012, ‘Why did Australia fare so well in the global financial crisis?’, pp. 203-300.
Himpler, JP 2018, ‘The World Financial Crisis: Impacts on GDP and international trade in Taiwan’, Crisis Management: Theory and Practice, p. 115.
Kandel, S, Ofer, AR & Sarig, O 1996, ‘Real interest rates and inflation: an ex‐ante empirical analysis’, The Journal of Finance, vol. 51, no. 1, pp. 205-225.
Kawai, M & Takagi, S 2011, ‘Why was Japan hit so hard by the global financial crisis?’, The impact of the economic crisis on East Asia: Policy responses from four economies, pp. 131-148.
Landefeld, JS, Seskin, EP & Fraumeni, BM 2008, ‘Taking the pulse of the economy: measuring GDP’, Journal of Economic Perspectives, vol. 22, no. 2, pp. 193-216.
Lepenies, P 2016, The power of a single number: a political history of GDP, Columbia University Press, New York City.
Levine, R & Zervos, S 1998, ‘Stock markets, banks, and economic growth’, American economic review, pp. 537-558.
Levine, R & Zervos, S 1999, Stock market development and long-run growth, The World Bank., Washington.
Liu, MH, Margaritis, D & Qiao, Z 2016, ‘The global financial crisis and retail interest rate pass-through in Australia’, Review of Pacific Basin financial markets and policies, vol. 19, no. 04, p. 1650026.
Mayer, C 1988, ‘New issues in corporate finance’, European Economic Review, vol. 32, no. 5, pp. 1167-1183.
Mishkin FS 2010, The economics of money, banking, and financial markets (9th ed), Pearson, Boston.
Mishkin, F. S. (1981). The real interest rate: an empirical investigation (No. w0622). National Bureau of Economic Research, Cambridge.
Mishkin, FS 1982, The real interest rate: a multi-country empirical study (No. w1047), National Bureau of Economic Research, Cambridge.
Sandte, H 2012, Stock markets vs GDP growth: a complicated mixture. Web.
Shafik, N & Jalali, J 1991, Are high real interest rates bad for world economic growth? (Vol. 669), World Bank Publications, Washington.
Shleifer, A. and Summers, L.H., 1988. Breach of trust in hostile takeovers. In Corporate takeovers: Causes and consequences (pp. 33-68). University of Chicago Press.
Stiglitz, JE 1985, ‘Credit markets and the control of capital’, Journal of Money, Credit and Banking, vol. 17, no. 2, pp. 133-152.
Suk Kim, B 2009, ‘The impact of the global financial crisis on Asia-Pacific real estate markets: evidence from Korea, Japan, Australia and US REITs’, Pacific Rim Property Research Journal, vol. 15, no. 4, pp. 398-416.
Sun, XQ, Shen, HW, Cheng, XQ & Zhang, Y 2016, ‘Market confidence predicts stock price: beyond supply and demand’, PloS one, vol. 11, no. 7, p. e0158742.
Tapscott, D 2015, The digital economy, McGraw-Hill Education, New York City.
Trabelsi MA 2011, ‘The impact of the financial crisis on the global economy: can the Islamic financial system help?’, Journal of Risk Finance, vol. 12, no. 1, pp. 15-25.
Wallison, PJ 2016, Hidden in plain sight: what really caused the world’s worst financial crisis and why It could happen again, Encounter Books, New York City.
Wang, B & Ajit, D 2013, ‘Stock market and economic growth in China’, Economics Bulletin, vol. 33, no. 1, pp. 95-103.
Watanabe, C, Naveed, K, Tou, Y & Neittaanmäki, P 2018, ‘Measuring GDP in the digital economy: increasing dependence on uncaptured GDP’, Technological Forecasting and Social Change, vol. 137, pp. 226-240.