Portfolio Selection Using Futures Arbitrage Pricing

Abstract

Arbitrage Pricing theories are a set of generalised methodologies used to calculate expected return on a riskless financial asset under different time-cost constraints which guarantee cash flow regardless of market direction. They find extensive application in diverse situations: inflation/GNP analysis, bonds, stocks, derivatives, commodities and foreign exchange currency trading etc.

In this dissertation, we aim to understand the application of arbitrage pricing opportunities in FX futures using the Black’s model for currency futures towards effective real-world situations involving a client company, X. The model will be tested for consistency using real data to measure any arbitrage opportunity for given time-cost constraints. The objective of this report is to present a methodical analysis of miscellaneous factors which can lay ground for evaluating profits at a given juncture.

Aims and Objectives

In this dissertation, we look at methods and opportunities to convert FX futures currency trading data into “cash flow” profits using Black’s arbitrage model for currency futures trading. This modelling technique is based on Black Scholes stochastic framework which calculates the relationship between different variables in the likelihood of extreme changes (volatility)¹. The following aims/objectives have been identified for the purpose of dissertation theme:

1. Designing an arbitrage model for currency futures trading in order to maximise profits and ensuring minimum arbitrage risk (Black’s model).
2. Testing the application of arbitrage model in a real-world scenario involving a client company, X which has close opportunities to maximise profits from FX trading (data has been collected from Datastream and company annual reports.).
3. Evaluating the success of chosen arbitrage model (Black’s model) and comparison with alternate theories of currency futures trading.

Methodology of research

The duties of an FX asset manager revolve around the ease and comfort with which he can understand the volatility and price opportunities connected with currency trading markets. As a student of Finance, I have worked on the following procedure as a way to ensure a good understanding of concepts included in successful application of arbitrage pricing methodologies for random business situations. According to the approach followed by a leading currency trading firm, Capgemini UK, the following methods are integral to the success of any evaluation strategy/theory connected with this topic (Capgemini UK, 2008):

1. Defining the Scope: This consists of defining the portfolio for which different projects are being assessed (Capgemini UK, 2008). In our case, it consists of “future pricing per minute data” for an assortment of currencies being traded by client company X (US $, Euro €, British Pound ₤ and Japanese Yen ¥). The small number of currencies selected for discussion imply their global value to forex investors as well as “simplicity” assumptions for modelling analysis techniques chosen.
2. Assessment: This consists of methods analysing project data through client interviews and assessing the project for delivery targets, risks and dependencies between projects (Capgemini UK, 2008). This is done using selective evaluation criteria on arbitrage pricing (Black’s model) through literature evidence.
3. Data Capture: Future pricing per minute has been selected from Datastream for developing currency projections for the given portfolio of currencies being traded by client company X (US $, Euro €, British Pound ₤ and Japanese Yen ¥).
4. Modelling: This consists of analysing required portfolio for fulfilling target objectives of a given arbitrage pricing model (Capgemini UK, 2008). The objective here is to assess individual project contributions to project delivery for overall delivery against target (Capgemini UK, 2008). This is consistent with our research objective number 3, evaluating the true success of the current model being used.
5. Scenario Analysis: It consists of maximising portfolio benefits using alt. theory.

Rationale of research

As a Master’s student of Finance, this dissertation enables me to test my knowledge in a subject of core interest: forex trading using relevant practical tools/methodologies. The conceptual tools used in this research include in-depth discussions on the chosen topic of arbitrage pricing techniques and reflects latest evaluation parameters. The purpose of choosing this dissertation topic is to develop a system which can be incorporated in our software. The methods and applications seek to demonstrate my conceptual skills and future learning activities.

Theoretical framework (Basics of Arbitrage Pricing Theory)

The Arbitrage Pricing theory for various financial instruments (including currency trading values) was originally invented by economist Stephen Ross in 1976 (Madura, 2006). The price of currency futures is normally held similar to the forward rate of a given currency and its settlement period in order to achieve potential arbitrage activity in case there is a chance of profit (p.126). This ensures if currency futures price on the pound is $ 2.00 and forward contracts are available for $1.98, firms may attempt to purchase forward contracts and simultaneously sell currency futures contracts (p.126).

If the firm can exactly match settlement dates for the given two contracts, it will ensure “guaranteed” profits worth $0.02 per unit. This will also allow downward pressure on the currency trading futures which to prevent any irreversible decline in currency exchange rates, one of the most salient benefits of arbitration techniques (p.126). Proper application of arbitrage techniques help in regulation of purchasing power parity between different currencies (p.126).

It should be kept in mind that currency futures price always differ from spot rates for the same reason forward contracts differ from their spot rates (p.126). If a currency’s spot and future prices were the same and the currency’s present exchange rate higher than the economy interest rate, this would give speculators an opportunity to maximise profits from their operations (p.126). This would give them the chance to purchase foreign currency at the spot rate and later, invest the funds at an attractive rate for the overall benefits of the concern (p.126). The currency futures can be simultaneously locked in at given exchange rate to be reconverted into original currency values (p.126).

In an ideal situation, if the spot and futures rates are the same, there would be neither a gain nor a loss on the currency conversion activities (p.126). Thus, the higher foreign interest rate becomes a safeguard to provide higher yield on such investment values (p.126). The actions of investors to capitalise on such opportunities place upward pressure on the spot rates and downward pressure on the currency futures price, causing the futures price to fall below the spot rate (p.126). In order to assess the wholesale impact of currency futures trading options, the following evaluation criteria will define the scope and assessment of our arbitration procedure (refer Methodology section on delivery targets, risks and dependencies between projects for the guidelines established by Capgemini UK).

Credit risk of currency future contracts

In any business transaction, risk assessment recieves top priority in overall market assesment criteria. For FX trading companies, each currency contract represents an “agreement” with the client even though the exchange has not been finalised (p.126). For example, if a broker is called on to contract with a settlement date in October 2008, the FX trading company will ensure neither party has to endure any arbitrary credit risks for the current futures trading position in given transaction (p.126).

In order to minimise risk in such guarantees, the Federal Reserve Bank is authorised to impose margin requirements to cover fluctuations in the value of the contract (p.126). This means participants will make a deposit with the brokerage firm while making a forward contract for the given period of settlement between the firms (p.126). This works in this way: if the value of futures contract “rises” over a given period of time, the seller has to pay the initial margin (p.126).

Conversely, if the value of futures contract “declines” over the same period of time, the buyer has to pay required margin for full and final settlement efforts (p.126). Margin requirements are not always mentioned for forward contracts in the scenario the bank authorises any “personal agreement” between buyer and seller (p.126).

Speculation about Currency futures

The salient feature of currency futures trading is the vast potential for business speculation and the ability to achieve profits using the same (p.127)². The intent here is to capitalise on expectations of a future currency movement (p.127). This is better understood using the following example – supposing, speculators assume the British Pound to appreciate in future, they will have to purchase a future contract which will lock in the price at which pounds are bought at a specified market rate (p.127). On the settlement date, it further leads to purchase of pounds at the rates specified by the futures contract and involves selling the currency at given spot rate (p.127). The idea here is if the spot rate has moved up in this given period of time, it would enable speculators to achieve maximum profits through the entire range of operations (p.127). It is thus, believed that,

“Currency futures are sold by speculators who expect the spot rate of a currency will be less than the rate at which they’ll be obligated to sell it” (Madura, 2006, p.127) This is further clarified using the following example. Supposing, as of October 4, 2008, a futures contract specifies 500,000 Japanese Yen for a December settlement period at a price of $.009. On October 4, 2008, the speculators who expected the Yen to decline with respect to the dollar sell future contracts on Yen (p.127). Assuming on the settlement date, the spot rates for the Yen is at $0.008, the gain on the futures position is automatically assessed to be $5,000 which represents the difference between selling Yen in accordance with the future contract versus the amount paid for Yen in spot market (p.127).

Above parameters are better decided using the criteria for marketing efficiency which indicates the ideal possibility that if the currency futures market is efficient, it automatically reflects all available information (p.127). Speculation efficiency refers to an unbiased estimate of a major currency’s impact on spot rate on the given settlement date (p.128). This means the continual use of a particular strategy to take positions in awarding currency futures contracts should not be held as the methodology to achieve abnormal profits on the given settlement indice (p.128).

Some positions will likely lead to profits whereas other positions will lead to losses (p.128), the point here being over a long period of time, gains and losses offset each other to give the speculator higher leverage and control over futures trading scenario (p.128). According to learnt experience in futures trading deals, the currency futures markets are generally assumed to be inefficient unless otherwise stated (p.128). The purpose of assessing speculation efficiency has a lot to do with organised trading activities which manoeuvre the happennings in the future trade (p.128).

Application of currency futures by firms

It is important for corporations to consider purchase/selling of futures contracts in different offsetting positions for the common purpose of profit realisation (p.128). The two most significant discussion parameters are:

1. Purchasing Futures to Hedge payables which reflects the ability of firms to future contract locks in the price at which it is able to purchase a currency (p.128).
2. Selling futures to hedge receivables which enables the selling of future contracts locks in the price at which it is able to sell a currency (p.128).
3. The last aspect of successful futures arbitration consists of a firm’s ability to “close out” a futures position when it has crossed its expectated return outcome values (p.129). The following parameters are integral to any discussion of assessing previous futures decisions with movements in spot rates for a given period of time (p.129).

If the spot rate of a currency increases over a given period of time, it indicates the ability of the FX index firm to correctly predict any rise in futures prices over a long period of time and hence, close the futures transaction successfully (p.129). The rise and fall of spot rates gives a unique perspective to aspirations of currency traders to evolve a holistic approach to correct prediction manoeuvres in currency trading (p.129).

Transaction costs are an integral aspect of achieving authentic futures trading scenario for given company evaluation criteria (p.129). In order to calculate transaction costs in a given situation, both traders and merging corporation perform necessary evaluation assessment on what constitutes a successful arbitration deal (p.133). This is seen in the wider context of operationalising deals worth a lot of money for both firms.

The objective of understanding literature evidence on various benefits/parameters of arbitrage trading is to achieve relevant benefits accruing from such study. In past discussions, it has been mentioned that the concepts derived from literature study contribute to our present volume of knowledge for application purposes. Here we summarise the required parameters which will be tested in case study example of company X featured in present discussions:

1. Understanding Credit Risks: This is done using greater analysis of margins trading for a given contract which is based on the principle of margin requirements for a given scale of operations: if the value of futures contract “rises” over a given period of time, the seller has to pay the initial margin otherwise he doesn’t have to pay anything. This principle will be used to assess required benefits of credit assessment for the sample company covered in research.
2. Understanding speculation risks: For the purpose of dissertation analysis, speculation risks will not be covered for the given company case study. As was discussed earlier, speculation risks are often measured by values consisting of speculation efficiency parameters. This is avoided in present discussions since modelling FX currency futures in combination with speculation risks leads to tedious combination of formulae and unnecessary parameters.
3. Applications of currency future trading: Potential applications of currency rate trading using hedging measures will be discussed for understanding market expectations behaviour for the given case study organisation. It is further held that these applications should revolve around a concerted effort to achieve real futures valuation for stated task needs.

Theoretical Framework-II (Mechanics/Model discussion)

As clarified in the outline, the Black’s model for Currency futures options discussion will be used to test and evaluate strategies for arbitrage evaluation in this paper. In order to fully comprehend the methodologies of arbitrage valuation tools, the following elements are important for our present discussion:

The Premium and Spot Exchange Rates (European Options)

The premium on a currency call option is generally considered higher when the exchange rate on the underlying currency is higher (Clark & Ghosh, 2004, p.56). This can be understood by the fact that when the spot exchange rate on the Dollar is say, Danish Kroner DKK 5.30, an investor should be more than willing to pay for the right to buy the dollars at DKK 5.00 than if the spot rate was 5.15 (p.56). On the other hand, the premium on a put is considered higher when the spot exchange rate on the underlying currency is lower (p.56). An investor will be willing to pay more for the right to sell dollars at DKK 5.00 if the spot rate is 4.85 rathern than 5.15 (p.56).

Despite the uncertain levels of exchange rate for given set of calculations, the premium on a call or put is always considered positive although it consists of arbitrarily small values (p.56). The reason is as long as there is a condition of expiry, there can be a remote possibility that something may happen to make the put option profitable (p.56). Even if the spot rate is DKK 5.00 and the strike price on a call within a week to expiration is DKK 7.50, uncertain events like natural catastrophes, wars etc. would push the exchange rate much above DKK 7.50 (p.56). If it doesn’t happen, the contract is said to “expire” (p.56). The right to a possible gain with no chance of loss is the biggest investment criteria subject to uncertainty (p.56).

For any arbitrary option on given spot rate, when the spot rate is very high compared to the strike price, the probability that the call option will be exercised is generally very high (p.57). Since, exercise uncertainty is defined as a direct measure of “decrease” in rise of spot rate, the value of an European call will tend to approach the value of the spot exchange rate minus the strike price (multiplied by the nominal amount of the contract) (p.57).

In such situations, the option will start to resemble a fixed forward contract where the strike price is considered equal to given forward rate (p.57). Similarly, if the spot exchange rate is assumed lower compared to strike price, the probability that a European put option will be exercised becomes very high (p.57). Its value starts approaching the difference between the strike price and the spot exchange rate (p.57).

Again, because of the high probability of realising put options in such scenarios, the option begins to resemble a fixed forward contract where the strike price plays the role of the forward rate for all calculation purposes (p.57). On the contrary, if the option is on a futures contract, the same arguments hold except that the futures rate replaces the spot rate in given formulation strategy (p.57).

The Premium and Spot Exchange Rates (American Options)

American Options are generally considered more complicated than European Options because unlike European expiry tags, they can be exercised anytime during the life of the organisation (p.58). When the spot exchange rate is very high compared to the strike price, it becomes advantageous for the call buyer to exercise before the expiration date of the option (p.58), especially if the forward exchange rate is at a heavy discount (p.58).

The reason for this is spot rate is usually at a much higher value compared to forward rate (p.58). In the given scenario where early exercising is possible, it is made advantageous to exercise early thus, when the forward rate is at a given discount value, the value of an American call option becomes higher than the value of an equivalent European option (p.58). The same argument can be extended for an American put option in which it is considered advantageous for a put buyer to exercise early when the ofrward rate is at a premium value (p.58). The Premium and the Strike Price: According to investor terms, a higher strike price gives a lower call value and a higher put value for other constraints being constant (p.59). On the other hand, a lower strike price gives a higher call value and a lower put value (p.59).

This is explained by the call for the right to buy the option at a given strike price, the lower the price, the more chances that the market price of the underlying currency will pass it for a profit (p.59). Conversely, since a put is the right to sell at a given strike price, the higher the price, the more the chance for market to regain the market price of given currency for equivalent values (p.59). At a lower strike price, the results are simply reversed (p.59).

When the strike price is considered higher than a given spot exchange rate, the value of a call is entirely due to its time value i.e. the possibility that the spot price will rise above the strike price before the option expires leads to an out-of-money condition where it is possible to see an immediate gain called intrinsic value which is equal to the difference between the spot rate and the strike price (p.59). On the other hand, if the strike price is lower than the spot rate, it leads to an immediate gain called the arbitrage value (p.59). It remains to be seen here that all the present value of the spot rate and the strike price are equal which gives an option called in-money, something used in the long run for settlement parameters (p.59).

The Premium and Exchange Rate Volatility

The volatility of the exchange rate is perhaps, the most important factor in determining the time value of a given put option (p.60). In all markets, traders tend to quote only those options which are described in terms of volatility than prices (p.60). The higher the volatility of the exchange rate, the higher the probability that a strong rise or fall would occur (p.60).

In terms of investor interests, this is the precise purpose that is achieved using a given put/call option (p.60). A sharp rise in exchange rates will be highly profitable for the owner of the call whereas a sharp fall in exchange rates will have just the opposite effect (p.60).

The outcome is similar for a put where the owner is looking for a fall in the underlying rate (p.60). The larger the fall, the greater the gain. On the other hand, if a sharp fall occurs, the owner loses nothing but the premium paid for given option (p.60). The outcome is similar for a put where the owner is hoping for a fall in given exchange rates (p.60). The larger the fall, greater the exchange rates (p.60). The value of a put always tends to increase with the volatility of underlying rates for given options available (p.60).

The Premium and the Expiry Date

Whenever the time to expiry is deemed longer, the chances for fluctuations in the exchange rate automatically increase, thereby leading to a rise in volatility for given stock scenario (p.60). It has to be brought to attention here that the expiry date has relevance for only European futures trading scenario (p.60). The objective of containing options for any similar events connected with the mechanisms of expiry cannot be seen in isolation from related discussions on miscellaneous arbitrage options uncovered in present study (p.60). The applications are being testsed as under.

According to literature evidence, whenever futures option and its underlying futures contract share a common expiry date, the value of futures option is given the same as an option on physical foreign exchange (DeRosa, 2000, p.159). This is because the futures option has no intermediate cash flows associated with owning it beyond the payment of the premium and because the futures price converges on the spot exchange rate at expiration value (p.159). In general scenario, futures option have shorter shelf lives than their associated deliverable futures contracts (p.159). For example, a futures contract that expires in Oct 2008 has a December futures contract (p.159). This is the reason a special model for currency futures option is needed and thus, the Black model steps in.

Black’s future options model for currency rates (European) involves three basic assumptions (indicative not exhaustive):

1. There are no taxes, no transaction costs and no restrictions on taking long or short positions in futures options or futures contracts (p.161). This means all transactors are price-takers and associated with a certain profit element (p.161).
2. The domestic interest rate is riskless and constant over the future’s option’s life (p.161). This indicates a lack of “speculation risks” outlined as a requirement in the previous section.
3. Instantaneous changes in the futures prices are indicated by the following differential equation: df/f = αdt + σdz where α is the drift term, dt is an instant in time and dz is a stochastic variable independent from time and is normal distributed with zero mean and standard deviation equal to the square root of dt (p.161). The basic purpose of citing these assumptions is to construct a local hedge for a long-term position in a currency futures call option using a short position in some number of currency futures contracts (p.161). As it is common in financial theory, the rate of return on the hedged position is assumed to be no more or no less than the risk free interest rate, R_d. This gives us Black’s Partial Differential Equation for Currency Futures Option as indicated by given formula (Fig.1, p.161):

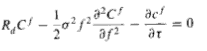
Above equation consists of boundary conditions for the value of European futures options which is given according to the following expiration values (Fig.2, p.162):

This basically indicates that at a given value of expiration, the value of either futures option is the greater of the zero and the amount by which the option is in the money (p.161) and thus, any relevant discussions on the subject should involve conditional probability criteria (p.163). This consists of a set of meaningful parameters which have been brought about to solve Black’s European futures option model for given test criteria used in the dissertation (p.163). In order to gain better understanding of the Black’s model, relevant discussions are based on parameters set by Clark & Ghosh (2004). The theories underpinning these pricing models consist of relevant payout options which make it a complete strategy evaluation as discussed hereunder.

Most options according to Black’s model are written on currency futures contracts. To price an option successfully, the following equation is discussed (Fig.3, p.73):

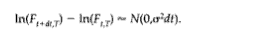
Here, F indicates return value for a given time period where N would indicate the natural logarithm of that time period (p.74). The Black’s model is a “continuous time model” for discussing currency rate arbitration under preceding criteria and can be defined in the context of a multitude of infinite small periods of time (p.69). This ability of Black’s model to achieve futures assessment over uneven time periods gives it the unique ability to accommodate diverse scenarios in currency trading for example, forward swaps, put and call options etc. (p.69). Apparently, there is no conflict between the real and imagined states of Black’s Model in a given test scenario.

Any theoretical discussions find a ready redemption in practical situations and thus, should be encouraged from the point of view of successful arbitrage endeavours (p.70). Supposing, the change of the logarithm of exchaneg rate in the time interval dt follows the normal law with the expected rate of return, Figure 3 as above can be rewritten as (Fig.4, p.69):

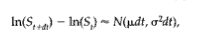
Here, S refers to the Spot Exchange Rate and N refers to natural logarithm as per Normal law. The hypothesis can have a series of interpretations: most studies will confirm that any change in exchange rates has two determinants: the first, dt which refers to deterministic evaluation of a well-known continuous economic phenomena. The second parameter refers to a random or stochastic evaluation element for the purposes of objective clarity.

Summary of Black’s Modelling Technique

It is been clearly shown in present discussions that the Black-Scholes model for evaluation of stochastic parameters discussed in our literature evidence project a far more important side of stochastic time-cost data analysis used for our applications. There is no doubt that the Blacks’ model can be used for easy calculation and explicit evaluation of different coordinate principles connected with equations (1-4) described here. Equation 1 (Fig.1) can be achieved only through partial differential equation method. For the purpose of our dissertation objectives, this would be solved using Mathworks’ Matlab software. Here is an objective summary of Black’s modelling for the purpose of given research objectives:

1. Black’s Partial Differential Equation to be solved –indicated by figure 1 which contains evaluating values for risk free interest rate, R_d as showcased in given study.
2. Boundaries of expiration for given futures values –indicated by figure 2
3. Return equations for currency trade values –indicated by figures 3 and 4 as described in our research study.

Application

Client X is a company dealing with FX trading since 1960 and is considered a major force to reckon with in the field of futures trading for various international. In order to fully understand the application of relevant discussions made out in the theoretical part, we must recapitulate the following aims/objectives outlined in this paper:

Defining the Scope

In our case, it consists of “future pricing per minute data” for an assortment of currencies being traded by client company X (US $, Euro €, British Pound ₤ and Japanese Yen ¥) (also see Appendix I questionnaire for understanding currency portfolio).

The small number of currencies selected for discussion imply their global value to forex investors as well as “simplicity” assumptions for modelling analysis techniques chosen. Since, the given set of currencies have arbitrary conditions in our evaluation assessment criteria, we follow the example of client company to understand its scope for 4 major world currencies.

Assessment

As discussed earlier, this consists of methods analysing project data through client interviews and assessing the project for delivery targets, risks and dependencies between projects (Capgemini UK, 2008). This was done using a set of interview questionnaires (see Appendix I), a few questions capture the core activities of the organisation for Client X – Put options, swaps, call options, forward contracts. Each and every activity has been defined according to the scope/potential of numerous business activities outlined by the group. In order to achieve results for theoretical references as mentioned before, the currency raw data is generated from suitable data generators.

Data Capture

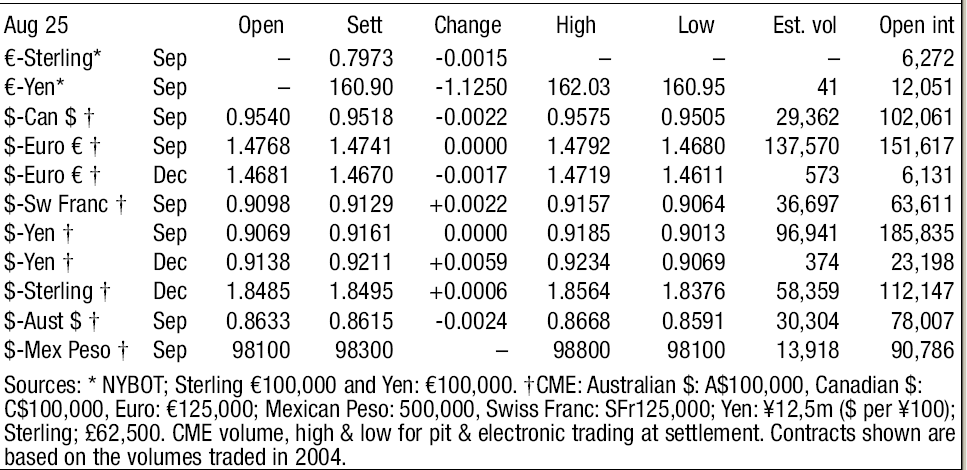
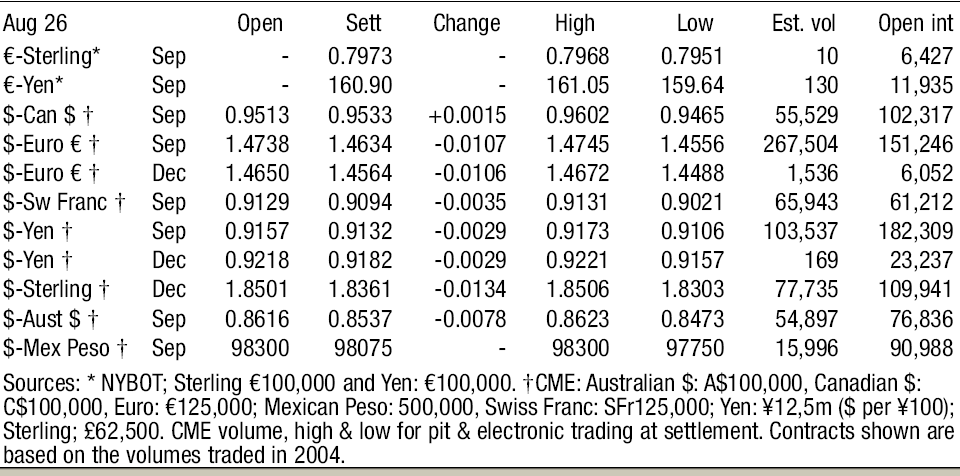
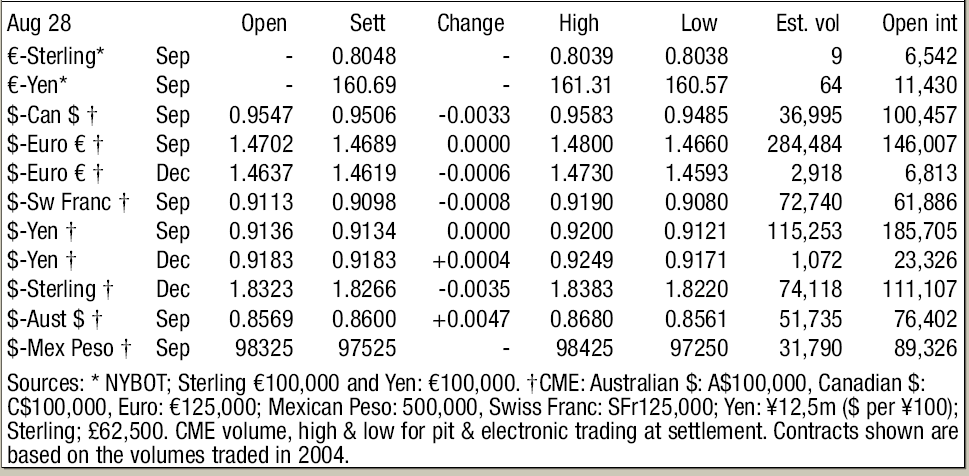
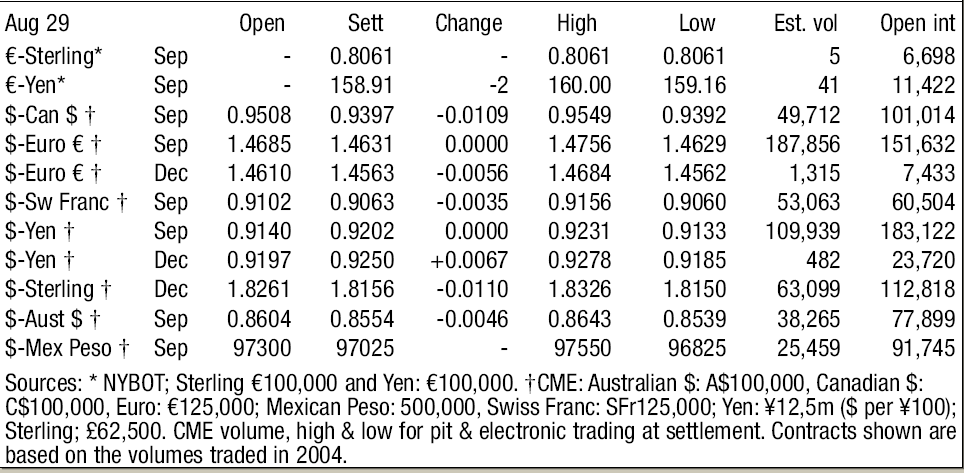
As discussed earlier, DataStream is the principal source used for collection of currency futures data and analysed later for the given portfolio of currencies defined in scope. The period of data capture runs between working days, Monday-to-Friday (25^th August to 29^th August, 2008). The complete set of currencies has been tabulated in Appendix II. The New York Board of Trade (NYBOT) is the principal commodities/futures exchange market used for reference in this time period. The raw data consists of highs and lows, open interest data and currency futures values (spot FX) adjusted by forward swaps (derived by interest rate differentials) to arrive at a future delivery price for the given set of currencies. In order to fully understand the particulars, the following concepts have to be clarified:

1. Open Interest: It refers to the total number of contracts entered into but not yet offset by a given transaction or delivery (Cheng, 2008). Any open interest held by a trader (in this case Client company X) is called a trader’s position whereas whenever a new buyer wants to establish a long position and buy a new contract, the open position is said to increase by one contract value (Cheng, 2008).
2. The Relationship between Open Interest and Price Trends: There is a surprising high degree of relationship between open interest rates in the futures market and price trends for our calculation/modelling purposes (Cheng, 2008). As a thumb rule, rising open interest rates points to a continuation of current price moves whereas fall in open interest rates points to the opposite (Cheng, 2008). This phenomena has been strongly reflected in Appendix II data and using investor methodology, the open interest data will be used to set precedence for different P.D.E. calculations as mentioned in theoretical framework.
3. The Change value: These are a crucial subset of futures values, varying between different day periods and used to assess the role of futures for short-term gains calculations. In order to fully illustrate the impact of short-term futures in the following discussion on modelling, the data tabulated has been put to good use for relevant states. The change values correspond directly to P.D.E. states.

Modelling

In order to gain a meaningful understanding of concepts connected with change values mentioned above, the model must reflect our theoretical discussions mentioned so far. The software tool used for this purpose is Mathworks’s Matlab which is a high-level language interactive environment designed to achieve faster solutions to numerous technical problems (Mathworks, 2008). The software is a “matrix laboratory” and interprets data by creating matrices of different dimensions using a pre-assigned syntax (program) (Goering, 2004).

Latest versions of the software obviate the need for pre-assigned syntaxes in favour of data arrays which roughly correspond to direct usage of tabular values as highlighted in Appendix II. For the purpose of modelling, let us summarise essential theoretical concepts from previous sections as follows:

The Premium and Spot Exchange Rates (American Options)

Since, the data is collected from NYBOT, we will be dealing with American Options. The spot exchange rates are described in “Sett” column of Appendix II. These rates indicate the premium at which these currency futures have been traded and should be dealt with in the future. The spot exchange rates are also used to keep track of numerous premium guarantees used to offset data constructs identified in the given period of time.

The raw data generated from appendix II will be further classified in order to generate and solve for partial differential equations in earlier sections of the report. In order to achieve clear-cut solutions to the problem, we shall undertake a thorough analysis of essential data-sets used to process raw data. The information used is in accordance with guidelines laid out by Client X (see scope and assessment parts of the Application section). The objective purpose of clarifying these trends is to achieve seamless integration of data-sets for complete assessment tasks.

Software Methodology

It will be also helpful to discuss and describe graphic presentation for software being used. Finding patterns in numbers is a mathematical and an intuitive undertaking (Mathworks a, 2008). When people collect data to analyze, they often want to see how models, variables, and constants explain hypotheses (Mathworks a, 2008). Sometimes they see by scanning tables or sets of statistics, other times by contemplating graphical representations of models and data (Mathworks a, 2008). An analyst’s powers of pattern recognition can lead to insights into data’s distribution, outliers, curvilinearity, associations between variables, goodness-of-fit to models, and more (Mathworks a, 2008). Computers amplify those powers greatly and thus, graphically exploring digital data interactively requires the following (Mathworks a, 2008):

1. Data displays for charts, graphs, and maps (Mathworks a, 2008)
2. A graphical user interface (GUI) capable of directly manipulating the displays (Mathworks a, 2008)
3. Software that categorizes selected data performs operations on the categories, and then updates or creates new data displays (Mathworks a, 2008).

This approach to understanding is often called exploratory data analysis

(EDA), a term coined during the infancy of computer graphics in the 1970s and generally attributed to statistician John Tukey (who also invented the box plot) (Mathworks a, 2008). EDA complements statistical methods and tools to help analysts check hypotheses and validate models (Mathworks a, 2008). An EDA GUI usually lets analysts divide observations of variables on data plots into subsets using mouse gestures, and then analyse further or eliminate selected observations (Mathworks a, 2008).

Part of EDA is simply looking at data graphics with an informed eye to observe patterns or lack of them (Mathworks a, 2008). What makes EDA especially powerful, however, are interactive tools that let analysts probe, drill down, map, and spin data sets around, and select observations and trace them through plots, tables, and models (Mathworks a, 2008). The tools/techniques used in various software modules provides us with a simplistic yet accurate portrayal of information sets used in computing analysis. In order to fully appreciate the impact of EDA, we shall consider their projections in different forms of data divisions derived from Appendix II.

The Expiry Date

Whenever the time to expiry is deemed longer, the chances for fluctuations in the exchange rate automatically increase, thereby leading to a rise in volatility for given stock scenario. In this particular scenario, we shall not be considering expiry dates for options as we are dealing with American options where expiry dates are not taken into account.

Black’s Partial Differential Equation for present scenario

The equation is written in general form as: R_dC^f – ½ * σ²f²* δ²C^f/ δ f² – δC^f/δτ where R_d indicates the rate of return, C^f indicates general coefficient terms, indicates standard deviation for given range of data. In this particular scenario, as discussed previously, we shall be using “open interest” valies indicated in Appendix II. This has to be further translated in accordance with the elementary rules of Matlab where we generate partial derivative equations.

The equations will be generated randomly out of trends indicated in currency futures values between 25 August- 29^th August. Before understanding the meaning of such trends, let us take a closer look into the elementary concepts of generating partial differential equations for “simulated” scenarios as indicated in present research. It is usually done using Matlab’s “Plots and Plotting Tools” menu where the data can be brought about to explore its features further (Mathworks a, 2008). With respect to present data analysis window, the various interactive tools eligible for customising MATLAB graphics are expressed as below:

• Loading data: The data is imported into workspace using “Load” function where it is further converted into “matrix” form for mathematical evaluation (Mathworks a, 2008). In our case, we have imported raw data “specific” to columns “open interest” and “sett” for each and every portfolio currency in define phase –US$, Euro, GBP and Yen. The changes in data set values which vary between two opposite rows has been further utlised to provide values for generating the P.D.E.
• Plotting the data: The data is plotted using the following command. It has to be noted here no programming skills are necessary to achieve the following command.

plot(t,count),

legend(‘Open Interest’,’Sett 2′,,2)

xlabel(‘Open Interest’), ylabel(‘Return Rd’)

• Using Statistical functions: The functions for Statistical tools in partial derivatives form is further utilised to achieve the following differential form for our given range of values related to open interest term R_d; it is further achieved through the software as follows:

R_d* 2.80145 –.369663* f²* δ²C^f/δ f² – δC^f/δt………………………………..(i)

Thus, we achieve target modelling for given range of data. NOTE: Boundary data used in section 2 has not been mentioned because that would require further usage of β values.

References

Capgemini UK, 2008, “Portfolio Modelling”, AGM Report (Capgemini UK), Vol. 32, 1187.

Cheng, G., 2008, “Forex: Gauging Forex Market Sentiment with Open Interest”, Investo- pedia. Web.

Clark, E. & Ghosh, D.K., 2004, Arbitrage, Hedging and Speculation, Greenwood Publishing Group. 69-73.

Data Stream, 2008, Future Currency values per Minute. Web.

DeRosa, D.F., 2000, Options on Foreign Exchange, John Wiley & Sons, New York, NY. 159-163.s.

Goering, R., 2004, “Matlab Edges Closer to Electronic Design Automation World”. Web.

Madura, J., 2006, International Financial Management, Thomson South-Western, UK. 129-133.

Mathworks, 2008, “About Matlab 7.6”. Web.

Mathworks a, 2008.

Appendix-I

Questionnaire for Client X company dealing with FX trading:

• Q1. What does your currency portfolio consist of? (Define phase)
  • Ans: (US $, Euro €, British Pound ₤ and Japanese Yen ¥)
• Q2. What are your major futures assessment activity?
  • Ans: Put options, swaps, call options, forward contracts
• Q3. Which source you recommend for data collection?
  • Ans: Data-Stream Publications
• Q4. Which software you recommend for analytical framework development?
  • Ans: MathWorks, Matlab Solutions for mathematical computation, analysis, visualisation and algorithm development
• Q5. Any relevant scenario analysis strategies?
  • Ans: To summarise the portfolio into a simplistic Euro-dollar combined structure: a Euro-dollars initiative

Appendix-II

Currency Futures Data at New York Board of Trade, a physical commodities exchange centre in New York City. Period of data capture: 25^th August, 2008-29^th August, 2008.

Footnotes

1. The Black-Scholes Model is a conventional technique used in Option-Pricing modelling analysis and can be applied to currency trading platforms. In analysing our specific dissertation objectives, we apply Black’s Arbitrage model which is a specific derivation of Black-Scholes model.
2. Speculation is an intrinsic part of currency arbitration benefits associated with FX futures trading.