Supply chain policy models have gotten much consideration from analysts recently. In this area, we concentrate on buyback policies, which are most firmly identified with this exploration. We allude to Cachon (2003) and Tsay et al. (1999) for audits of different kinds of supply chain policies.
Buyback policies, which are also called returns policies, are standard in the appropriation of perishable items with questionable request, for example, books, magazines, daily papers, recorded music, PC hardware and programs, greeting cards, and pharmaceutical products (Padmanabhan and Png, 1995). Pasternack (1985) is the first to concentrate on buyback policies. He demonstrates that the two extremes, full returns with full buyback credit and no profits, are framework imperfect; however, he notes that the supply chain can be facilitated by a moderate buyback policy (e.g., incomplete returns with full buyback acknowledgement or full returns for halfway buyback credit). He additionally recognizes a class of buyback policies with coordinating parameters that are independent of market demand. Kandel (1996) broadens Pasternack’s (1985) findings to a value-sensitive stochastic request model and presumes that the supply chain can’t be comprised of buyback policies without retail value upkeep (i.e., enabling the producer to direct the retail cost). Emmons and Gilbert (1998) concentrate on a cost-sensitive multiplicative model of interest uncertainty for list merchandise and show that instability tends to increase the retail cost. They likewise demonstrate that, under specific conditions, a manufacturer can expand benefits by offering a buyback policy. Webster and Weng (2000) take the view-purpose of a producer pitching to a solitary retailer and depict chance-free buyback policies. Donohue (2000) considers buyback policies in a supply chain model with numerous production openings and enhancing request estimates. Taylor (2002) unites a buyback policy with an objective deals refund policy to facilitate the supply chain when a request is delicate to the retailer deals exertion.
Notwithstanding the risk, a few analysts have considered supply chain policies in light of the customary principal-agency hypothesis that fuses risk avoidance. Agrawal and Seshadri (2000) explore a supply chain made out of a risk-neutral merchant and risk-averse retailers for a short-lifecycle product, where the wholesaler offers a risk intermediation policy with a settled expense, a discount cost for every unit sold, and a buyback cost for every unit unsold, so as to instigate the risk-averse retailers to arrange their benefit amplifying amounts. Plambeck and Zenios (2000) concentrate on a dynamic principal-agent model with the physical structure of a Markov choice process that is not the same as the newsvendor model setting in our article. They demonstrate that the risk-neutral principal can outline an ideal installment plan to instigate the risk-averse operator’s activities and revenue-driven expansion. While those works are based on the customary principal-agency hypothesis that fuses risk avoidance, this article draws on the behavioral principal-agency hypothesis that fuses loss aversion. Loss aversion comes from the field of brain science and can be traced to the work of Kahneman and Tversky (1979). It is distinguished from risk avoidance by the proximity of a reference point that decides whether a result is viewed as a loss or a gain and by an unexpected change in the incline of the utility capacity at the reference point. We refer interested scholars to Wiseman and Gomez-Mejia (1998) and references in that dialogue of the contrast between the conventional and behavioral principal-agency hypotheses.
Supply Chain Model
The starting point would be the research on a vertically integrated firm. One of the core components of such firm would have to be a large and diversified manufacturer that would not perceive possible risk as a significant obstacle. This manufacturer would also have to perform central planning for the supply chain. The manufacturer’s control would provide a benchmark solution that increases the supply chain’s contribution.
As soon as the selling is at its peak (the beginning of the selling season), the integrated firm produces a certain amount of a single item (Q). The units’ cost is not affected by its quantity; the cost is marked as c. The units are then sold at their retail price p which must be naturally higher than the cost c. The demand is X; it is a random variable with PDF f(x) and CDF F(x), which must be calculated during a specific time period I ∈ [0, ∞). The tail distribution is defined by the following equation F¯ (x) = 1 − F(x). F(x) is expected to be able to increase over the abovementioned time period I, while also remaining invertible and differentiable. If X > Q is true, the profits made by X – Q units are negated. Unsatisfied demands are expected to result in no further costs likewise in the models formulated by other researchers (for example, in Lariviere and Porteus, 2002; Netessine and Zhang, 2005). Furthermore, if X < Q is true, the integrated firm would return Q – X unrealized units at a v < c value. The firm would then expect a system profit formulated by the following equation:
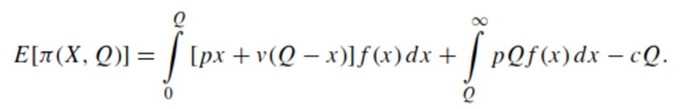
However, it would require product quantity to maximize profit according to:
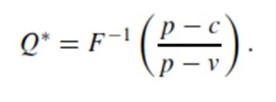
The opposite model would be that of a large independent manufacturer cooperating with a small independent retailer. The manufacturer, as in the first case, is risk neutral. Retailer, in turn, prefers to avoid risks despite their possible beneficial nature. Q units of a single product are ordered from the manufacturer. The price is w, manufacturer’s cost for delivery and production is c which is less than w. The retail price, in turn, is p > w. W0 refers to retailer’s initial wealth. The gain or loss is then evident if the profits made are higher or lower that the starting capital. The retailer’s utility in avoiding risks is linear:
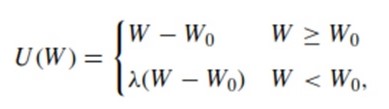
λ ≥ 1is the level of risk avoided. If λ = 1, retailer’s risk avoidance remains on a neutral level. Further increases in λ indicate higher levels, and if λ remains relatively close to 1, then – at the reference level – there is a slope change. W is the retailer’s final capital. Without any losses in generality, W0 = 0 may be considered normal. This form of loss-aversion is commonly referred to by researchers because of its simplistic nature (Kahneman and Tversky, 1979). It does not preserve the decreasing sensitivity aspect in prospect theory.
If retailer is able to sell a v < w for each unrealized unit, the retailer’s expected profits (price-only contract) are:
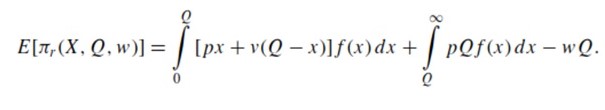
The retailer’s ability to avoid losses is defined by:
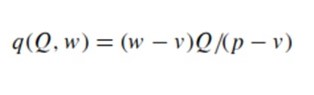
This functions if the amount of product sold relative to Q is not high enough. If realized products are, in fact, more than q(Q, w), the profits increase. After (4) is mapped to (3), the retailer’s utility E[U(πr(X, Q,w))] is:
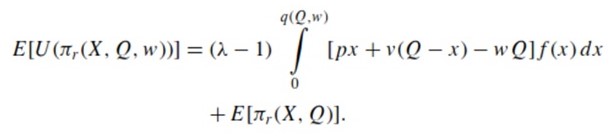
This expresses the retailer’s expected utility under the price-only contract. If λ = 1, the first term of (6) is negated.
After the first and second derivative of (6) are juxtaposed to Q, the following formula is derived:
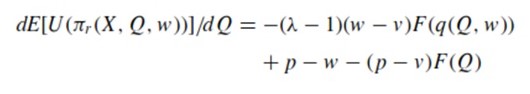
which results in
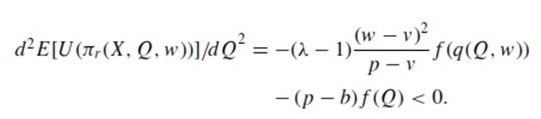
Thus, the retailer is expected to have a concave expected utility. The retailer’s optimal amount of ordered products under the price-only contract Q∗λ−1 would be derived from dE[U(πr(X, inf I,w)]d Q > 0 and dE[U(πr(X,sup I,w)]/d Q < 0 and is a unique and finite static point in I. However, the following condition must be met

If the retailer avoids risks, the retailer’s optimal amount of ordered products Q*0 is also unique under the following first-order condition
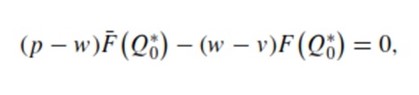
The conclusion is the standard newsvendor result
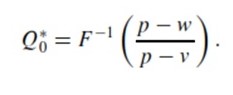
After comparing (2), (7), and (8) there occurs a possibility of determining two main sources of inventory under-stocking for the decentralized supply chain for both risk avoiding retailer and retailer that does not take risk into account as much. The first one is reflected in the first term of (7) and is stipulated by the loss aversion. The second one is presented in the second term of (7) and is a result of double marginalization. Both make the optimal products ordered number less, resulting in λ > 1, Q∗λ−1 < Q∗0 < Q∗. This results in decreasing profits for this type of supply chain with a retailer avoiding risk. If the supply chain is integrated or decentralized, and the retailer does not avoid risk, the profit is, in fact, expected to be higher.
Bibliography
Agrawal, Vipul, and Sridhar Seshadri “Hazard intermediation in supply chains,” IIE Transactions 32 no. 9 (2000): 819–931.
Cachon, Gerard P, (2003). “Supply chain coordination with contracts.” In Handbook in operations research and administration science, volume on supply chain administration: Design, coordination and operation. Edited by A. G. de Kok and S. C. Graves 229-339 (Amsterdam: North Holland, 2003).
Donohue, Kathlyn. “Effective supply contracts for form merchandise with conjecture refreshing and two creation modes. Administration Science 46, (2000): 1397–1411.
Emmons, Hamilton, and Stephen M. Gilbert, “Note. The part of profits approaches in valuing and stock choices for index merchandise.” Administration Science 44, no. 2 (1998): 276–283.
Kahneman, Daniel, and Amos Tversky, “Prospect hypothesis: An investigation of choices under hazard,” Econometrica 47, no. 2 (1979): 263–291.
Kandel, Eric, “The privilege to return.” Diary of Law and Economics 39, (1996): 329–356.
Lariviere, Martin An., and Evan L. Porteus, “Pitching to the newsvendor: An investigation of cost just contracts.” Assembling and Service Operations Management 3, no. 4 (2002): 293–305.
Netessine, Serguei S., and Fuqiang Zhang “Positive versus negative externalities in stock administration: Implications for supply chain plan”. Assembling and Ser-bad habit Operations Management 7, no. 1, (2005): 58–73.
Padmanabhan, Paddy V., and Ivan I. P. Png, “Returns arrangements: Make cash by making great.” Sloan Management Review 37, no. 1 (1995): 65–72.
Pasternack, Bruce A. “Ideal valuing and merchandise exchanges for perishable com-modities”. Promoting Science 4, no. 2 (1985): 166–176.
Plambeck, Erica L., and Stavros A. Zenios, “Execution based motivating forces in a dynamic rule organization display,” Assembling and Service Operations Management 2, (2000): 240–263.
Taylor, Terry A. “Supply chain coordination under channel refunds with deals exertion impacts.” Administration Science 48, no. 8 (2002): 992–1007.
Tsay, Andy A., Steven Nahmias, and Narendra Agrawal “Displaying supply chain con-tracts: A survey.” In Quantitative models for supply chain administration edited by S. Tayur, R. Ganeshan, and M. Magazine 299-336 (Boston: Kluwer Academic, 1999).
Webster, Scott, and Z. K. Weng, “A hazard free perishable thing returns arrangement.” Assembling and Service Operations Management, 2, (2000): 100–106.
Wiseman, Robert M., and Luis R. Gomez-Mejia (1998). “A behavioral organization model of administrative hazard taking.” The Academy of Management Review 23, no. 1, (1998): 133–153.