Introduction
Trade is one of the activities that foster the growth of the human society. Since the time immemorial, people have used various trade systems with an aim of exchanging surplus commodities amongst localities. This essay discusses the classical theory of trade with respect to Ricardian comparative advantage and influence on the post-Bretton Woods Agreement on General Agreement on Trade and Tariffs.
Ricardian Comparative Advantage after the Bretton Woods Agreement on General Agreement on Trade and Tariffs (GATT)
The GATT result from the Bretton Woods Agreement
A Bretton Wood Conference established the GATT as part of the agreements to initiate the International Trade Organisation (ITO). The GATT was assumed to reduce various trade barriers such as high tariffs among others. Another promise to be undertaken by countries under the umbrella of GATT is the acceptance of various principles that are in tandem with the international policies on trade (Dominguez, 1993). Furthermore, there is existence of the relative ratios of labour that influences the production of commodities differs from one country to another. Lastly, the model assumes that a perfect competition exist in the economy (Dominguez, 1993).
Comparative advantage
David Ricardo serves postulated the idea of comparative advantage as a solution of mutual benefits in trade. Ricardo’s assumptions in his Ricardian model include; labour that is considered as the primary source of value in the production, there exists a constant Marginal product of Labour (MPL). This situation implies that constant productivity of labour, return to scale, and technology are not complex (Griffiths, Zhang, & Zhao, 2014). The model also assumes that labour is limited and mobile in various sectors internally. However, such situations do not exist internationally (Dominguez, 1993).
Two countries (A and B) are involved in a trading system. The commodities produced by both nations are tea and pyrethrum. The costs of production are summarised as follows.
It can be noted from the table that a unit of pyrethrum in country A costs the same amount to produce 3 units of tea. There is an opportunity cost incurred in producing pyrethrum since the country misses 3 units of tea. In country B, the opportunity cost of producing pyrethrum is 0.83 units of tea. Due to such it can be said that both countries have comparative advantages in producing tea and pyrethrum respectively (Appleyard, Cobb, & Field, 2014).
Analysis of the effects of wages, productivity, and exchange rates on the model of comparative advantage and international trade patterns
Pattern of trade and labour productivity
A major factor that enables countries to trade is the ability to achieve the economies of scale in its production and their differences (Deardorff, 2001). Comparative advantage is better understood when economy is examined in terms of the factors of production (Appleyard et al., 2014). Due to the inadequate resource of various countries, emphasis is laid on the minimisation of what a country is supposed to produce to ensure tradeoffs. The technique of a trade-off requires a sacrifice to be done on a particular item for another. It is demonstrated using the production possibility frontier as shown below.
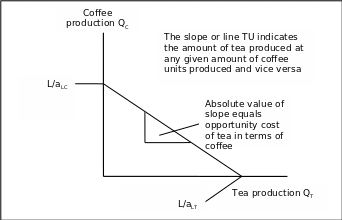
A productivity frontier of a country’s economy indicates a straight line if only one production factor exists. The derivation of the TU line can be done by the formation of an equation. QC is the quantity production of coffee and QT is the production quantity of tea. The labour required to produce coffee will be as follows; aLCQC and that of production of tea is aLTQT. The limiting factor that is considered is the labour indicated by L. This limit of production offers production possibility a frontier. It is derived using the following equation (Griffiths et al., 2014):
- = aLCQC + aLTQT ≤ L (Pugel, 2012).
If labour supply produced by the country above is 4000 hours, and it takes 2 hours of labour to produce a unit of tea and 4 hours of labour to produce a unit of coffee, the total labour used in production is achieved as follows:
- (2 x units of tea) + (4 x units of coffee) = the total must be less or equal to the 4000 hours of labour available (Pugel, 2012).
If the country uses its resource to produce only tea, then it will be L/aLT units. If the same is done on coffee, then it will be L/aLC units. Therefore, a person who takes 4 hours to produce a unit of coffee must sacrifice 2 units of tea. This practice is called the opportunity cost. The opportunity cost can be minimised through the utilisation of comparative advantage in trade (Pugel, 2012; Griffiths et al., 2014).
Assuming the country M and a new country N, the labour force of the country N is NL. The unit labour needed to produce tea and coffee will be denoted as aNLT and aNLC respectively. The workforce requirement for the two nations can follow specific directions. For example, country M can be less productive when it comes to coffee than country N or the other way round. One assumption can be derived at as follows.
- = aLT/aLC < aNLT/aNLC or aLT/aNLT < aLC/aNLC (Appleyard, Cobb, & Field, 2014).
From the two equations above, country M can also have a comparative advantage in tea production under four labour requirement units (Pugel, 2012; Teece, 2014).
Price Determination using the Comparative Advantage
Price determination in all kinds of trade is based on the demand and supply techniques. A comparative advantage ensures the relationship in markets. For instance, country M exports tea to get coffee and country N exports coffee in return to get tea. It is required to analyse the prices in terms of general equilibrium that links the two markets. Keeping record tracks of relative supply and demands and the supply and demands for tea and coffee can help in the determination of prices (Pugel, 2012).
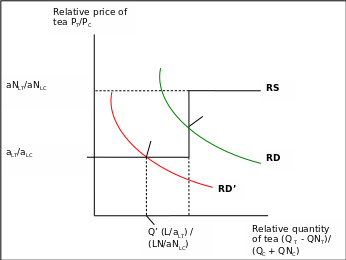
The RD and RD’ curves indicate the demand for tea in relation to coffee in a reducing function of price of tea relative to coffee. The SD curve indicates supply of tea relative to coffee in an increasing function of same relative prices (Deardorff, 2001).
The relative supply curve RS is step-shaped. The RS curve indicates that no supply of tea if the global price drops below aLT/aLC. It comes as a result of specialisation in production of coffee by country N and specialisation of production of tea by country M and an assumption of aLT/aLC < aNLT/aNLC . Therefore, relative prices of tea result in zero production. Whenever the relative price of tea PT/PC is at aLT/aLC, the labourers in country M earn the same amount of wages in either product. Country M is in a position to supply either the goods in the market. This situation is represented by the flatness sections of relative supply curve (Deardorff, 2001).
When PT/PC is above aNLT/aNLC, country M specialises in tea production at L/aLT units. At any given moment PT/PC < aLT/aLC, country N specialises in producing coffee at LN/aNLC units. It can be concluded that at any relative price of tea between aNLT/aNLC and aLT/aLC the relative supply of tea is ( L/aLT) / (LN/aNLC) (Deardorff, 2001).
When PT/PC equals aNLT/aNLC, the workers in country N have same wages in either production of tea or coffee. This situation is indicated by a flat curve. Lastly, when PT/PC > aNLT/aNLC, the two countries shall specialise in tea production (Deardorff, 2001).
Gains in trade due to comparative advantage
Gain in trade comes into play due to the technique of specialisation. Countries see trade as an indirect way of production. For example, country M can indirectly produce coffee by exporting tea. Indirect production reduces the chances of occurrence of opportunity costs. Trade also ensures the possibility of a country to consume a particular commodity. In the absence of trade, there is a similar result in the consumption possibility to that of production. When trade takes place, there is a mix of consumption possibilities due to the expansion of choices (Pugel, 2012).
Wages and exchange rates in relation to comparative advantage
Wage rates in international trade have been a factor that is considered in terms of politics. Comparisons are always made among the trading nations on the recommended wages of workers in either nation. For example, a comparison of wage rates between Mexico workers and those of United States (Appleyard et al., 2014).
A comparison of wage rates can be done using the examples above. Due to specialisation, the workers in Country M were able to produce tea. It takes 2 hours to produce a unit of tea. Therefore, the labourers get their wages the value of ½ a unit of tea in 1 hour. The labourers from country N earns the value of ¼ unit of coffee in 1 hour. If the exchange rates of both tea and coffee in terms of dollars are $ 32, then the workers of country M will earn $ 16 dollars per unit of tea in 1 hour while their counterparts in country N will earn $ 8 per unit of coffee per hour (Appleyard et al., 2014).
Conclusion
The essay has analysed the efficiency of the Ricardian model of comparative advantage with respect to GATT. It has also highlighted how wage rates, trade and productivity influence the model by use of elaborative examples. This model is always used in the international trade systems to understand the gains in free trade and the various international economic policies. The Ricardian model is therefore effective in influencing international trade.
Reference List
Appleyard, D., Cobb, S., & Field, A. (2014). International economics. New York, NY: McGraw-Hill.
Deardorff, A. (2001). International provision of trade services, trade, and fragmentation. Review of International Economics, 9(2), 233-248.
Dominguez, K. (1993). The role of international organisations in the Bretton Woods system. New York, NY: University of Chicago Press.
Griffiths, W., Zhang, X., & Zhao, X. (2014). Estimation and efficiency measurement in stochastic production frontiers with ordinal outcomes. Journal of Productivity Analysis, 42(1), 67.
Pugel, T. (2012) International economics. New York, NY: McGraw-Hill.
Teece, D. (2014). The nature and consequences of trade-off transparency in the context of recommendation agents1. Academy of Management Perspectives, 28(4), 328-52.